To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Michaelis-Menten kineticsMichaelis-Menten kinetics describes the kinetics of many enzymes. It is named after Leonor Michaelis and Maud Menten. This kinetic model is relevant to situations where the concentration of enzyme is much lower than the concentration of substrate (i.e. where enzyme concentration is the limiting factor), and when the enzyme is not allosteric. Product highlight
HistoryThe modern relationship between substrate and enzyme concentration was proposed in 1903 by Victor Henri. [1] A microscopic interpretation was thereafter proposed in 1913 by Leonor Michaelis and Maud Menten, following earlier work by Archibald Vivian Hill.[2] It postulated that enzyme (catalyst) and substrate (reactant) are in fast equilibrium with their complex, which then dissociates to yield product and free enzyme. The current derivation, based on the quasi steady state approximation, namely that the concentrations of the intermediate complexes do not change, has been proposed by Briggs and Haldane.[3] Determination of constantsTo determine the maximum rate of an enzyme mediated reaction, a series of experiments is carried out where the substrate concentration ([S]) is increased until a constant initial rate of product formation is achieved. This is the maximum velocity (Vmax) of the enzyme under the conditions of the experiment. In this state, enzyme active sites are saturated with substrate. Reaction rate/velocity VThe reaction rate V is the number of reactions per second catalyzed per mole of the enzyme. The reaction rate increases with increasing substrate concentration [S], asymptotically approaching the maximum rate Vmax. There is therefore no clearly-defined substrate concentration at which the enzyme can be said to be saturated with substrate. A more appropriate measure to characterise an enzyme is the substrate concentration at which the reaction rate reaches half of its maximum value (Vmax/2). This concentration can be shown to be equal to the Michaelis constant (KM). Michaelis constant 'KM'For enzymatic reactions which exhibit simple Michaelis-Menten kinetics and in which product formation is the rate-limiting step (i.e., when k2 << k-1) KM≈k-1/k1=Kd, where Kd is the dissociation constant (affinity for substrate) of the enzyme-substrate (ES) complex. However, often k2 >> k-1, or k2 and k-1 are comparable, in which case nothing can be said about the enzyme affinity from the Michaelis constant alone.[4] EquationThe most convenient derivation of the Michaelis-Menten equation, described by Briggs and Haldane, is obtained as follows: The enzymatic reaction is assumed to be irreversible, and the product does not bind to the enzyme.
The rate of production of the product, d[P] / dt is referred to as the reaction rate, V in enzyme kinetics. It is dependent on the conversion rate constant, k2 (often referred to as the catalytic constant, kcat) and [ES], the concentration of enzyme that is bound to substrate. As [ES] is not usually measurable, it must be expressed in terms of the known parameters of the system, namely the concentration of enzyme and substrate originally added. A key assumption in this derivation is the quasi steady state approximation, namely that the concentration of the substrate-bound enzyme (and hence also the unbound enzyme) change much more slowly than those of the product and substrate. This allows us to express the relationship between the substrate concentration and the bound and unbound enzyme concentrations in terms of the various rate constants:
To simplify the equation, we define the Michaelis constant as:
yielding:
The total concentration of enzyme ([E0]) is the sum of the free enzyme in solution ([E]) and that which is bound to the substrate ([ES]), allowing us to derive the free enzyme concentration from (1): [E0] = [E] + [ES] [E] = [E0] − [ES] (2) Using this concentration (2), the bound enzyme concentration (1) can now be written:
Rearranging gives:
The reaction rate is:
Substituting (3) in (4) and multiplying the numerator and denominator by [S] gives:
Because the concentration of substrate changes as the reaction takes place, the initial reaction rate (V0) is used to simplify analysis, taking the initial concentration of substrate as [S].
This equation may be represented by a Lineweaver-Burk plot or a Hanes-Woolf plot. If [S] is large compared to Km, [S]/(Km + [S]) approaches 1. Therefore, the rate of product formation is equal to k2[E0] in this case. When [S] equals Km, [S]/(Km + [S]) equals 0.5. In this case, the rate of product formation is half of the maximum rate (1/2 Vmax). By plotting V0 against [S], one can easily determine Vmax and Km. The most common way of generating this data is with a series of experiments at constant E0 and different substrate concentration [S]. The Michaelis-Menten equation describes the rates of irreversible reactions. A steady state solution for a chemical equilibrium modeled with Michaelis-Menten kinetics can be obtained with the Goldbeter-Koshland equation. LimitationsMichaelis-Menten kinetics, like other classical biochemical kinetic theories, relies on the law of mass action derived from the assumptions of free (Fickian) diffusion and thermodynamically-driven random collision. However, many biochemical or cellular processes deviate significantly from such conditions. For example, the cytoplasm inside a cell behaves more like a gel than a freely flowable or watery liquid, due to the very high concentration of protein (up to ~400 mg/mL) and other “solutes”, which can severely limit molecular movements (diffusion or collision) (see e.g. Olsen [5]). For heterogeneous enzymatic reactions, such as those of membrane enzymes, molecular mobility of the enzyme or substrates can also be severely restricted, due to the immobilization or phase-separation of the reactants. For some homogeneous enzymatic reactions, the mobility of the enzyme or substrate may also be limited, such as the case of DNA polymerase where the enzyme moves along a chained substrate, rather than having a three-dimensional freedom. The limitation on molecular mobility (as well as other “non-ideal” conditions) demands modifications on the conventional mass-action laws, and Michaelis-Menten kinetics, to better reflect certain real world situations. Although it has been shown that the law of mass action can be valid in heterogeneous environments (see, R. Grima and S. Schnell [6]). In general physics and chemistry, limited mobility-derived kinetics have been successfully described by the fractal-like kinetics. R. Kopelman [7], M.A. Savageau [8], and S. Schnell [9] pioneered the “fractal enzymology”, which has been further developed by other researchers.[10] References
Further reading
Categories: Enzyme kinetics | Chemical kinetics |
|||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Michaelis-Menten_kinetics". A list of authors is available in Wikipedia. | |||||||





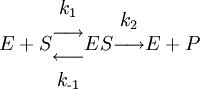
![[ES] = \frac{k_1[E][S]}{k_{\textrm{-}1} + k_2}](images/math/5/6/4/564101d3962382ba35ca6853f00f0374.png)
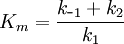
![[ES] = \frac{[E][S]}{K_m}](images/math/0/6/7/067e112a39ebb7ff143866a36bad4b6f.png) (1)
(1)
![[ES] = \frac{([E_0] - [ES]) [S]}{K_m}](images/math/6/1/0/6106c8382e6fcce1a66cf6844de78b21.png)
![[ES] \frac{K_m}{[S]} = [E_0] - [ES]](images/math/3/c/e/3ce22a467b183a7587f024bdfb5f4802.png)
![[ES]\left(1 + \frac{K_m}{[S]}\right) = [E_0]](images/math/5/0/b/50b4b563da2299f3f125434a8c5e7339.png)
![[ES] = [E_0]\frac{1}{1+\frac{K_m}{[S]}}](images/math/8/7/9/879800acc78fd45e3f9287faf9c5ddcb.png) (3)
(3)
![V = \frac{d[P]}{dt} = k_2[ES]](images/math/d/d/5/dd58a6c923e8f25250abc664f42b333b.png) (4)
(4)
![\frac{d[P]}{dt} = k_2[E_0]\frac{[S]}{K_m + [S]} = V_{max}\frac{[S]}{K_m + [S]}](images/math/6/f/b/6fb713b192f50c8136572a36dcb3d905.png)


