Navier-Stokes existence and smoothness
The Navier-Stokes equations, which describe the flow of ordinary fluids such as water, can be extremely complicated and difficult to solve. Numerical solutions to these equations are frequently used in many fields, such as aircraft design and weather forecasting. However, the theory behind these solutions is unsatisfactory. For the three dimensional system of equations, mathematicians have proved neither that smooth solutions always exist (existence), nor that if they do exist they do not contain any infinities or singularities (smoothness). Showing that solutions exist, and that they are smooth, is therefore called the Navier-Stokes existence and smoothness problem. A $1,000,000 prize was offered in May 2000 by the Clay Mathematics Institute to whomever proves any of the following statements about the Navier-Stokes equations.
| Millennium Prize Problems
|
| P versus NP
|
| The Hodge conjecture
|
| The Poincaré conjecture
|
| The Riemann hypothesis
|
| Yang–Mills existence and mass gap
|
| Navier-Stokes existence and smoothness
|
| The Birch and Swinnerton-Dyer conjecture
|
Problem description
Let 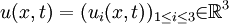 be the unknown velocity vector field, defined for positions be the unknown velocity vector field, defined for positions 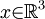 and times and times 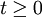 and let and let 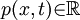 be the unknown pressure, defined likewise. be the unknown pressure, defined likewise.
Let 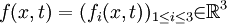 be a known external force, again defined for positions be a known external force, again defined for positions 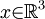 and times and times 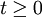 . .
Also let 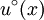 be the known initial velocity vector field on R3, which is divergence-free on C∞. be the known initial velocity vector field on R3, which is divergence-free on C∞.
Finally, let ν > 0 be a known constant (the viscosity).
Then the Navier-Stokes equations for incompressible viscous fluids filling R3 are given by 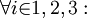
|
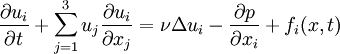
| 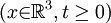
| (1)
|
Where Δ is the Laplacian in the space variables.
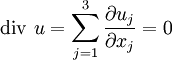
| 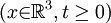
| (2)
|
And the initial condition:
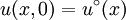
| 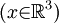
| (3)
|
The problem then is to prove one of the following four statements:
(A) Existence and smoothness of Navier-Stokes solutions on 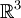
Assume in addition that:
- There are no external forces, i.e.:
-
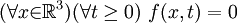
-
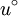 is bounded, i.e.: is bounded, i.e.:
-
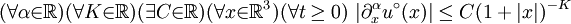
Then there exists 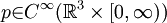 and and 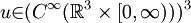 that satisfy (1), (2) and (3) as well as having bounded energy, i.e.: that satisfy (1), (2) and (3) as well as having bounded energy, i.e.:
-
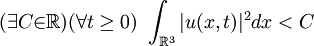
(B) Existence and smoothness of Navier-Stokes solutions on 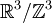
Assume in addition that:
- There are no external forces, i.e.:
-
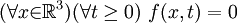
-
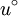 is periodic, i.e.: is periodic, i.e.:
-
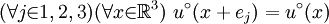 , where ej is the jth unit vector in R3. , where ej is the jth unit vector in R3.
Then there exists 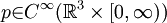 and and 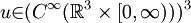 that satisfy (1), (2) and (3) and have a periodic u, i.e.: that satisfy (1), (2) and (3) and have a periodic u, i.e.:
-
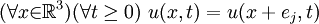
(C) Breakdown of Navier-Stokes solutions on 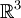
There exists an 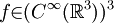 and a divergence-free and a divergence-free 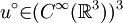 for which there are no for which there are no 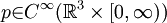 and and 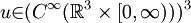 satisfying (1), (2), (3) and also having bounded energy, i.e.: satisfying (1), (2), (3) and also having bounded energy, i.e.:
-
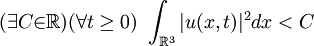
(D) Breakdown of Navier-Stokes solutions on 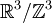
There exists an 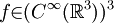 and a divergence-free and a divergence-free 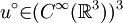 for which there are no for which there are no 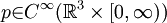 and and 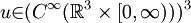 satisfying (1), (2), (3) and also having a periodic u, i.e.: satisfying (1), (2), (3) and also having a periodic u, i.e.:
-
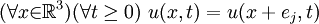
Background
The analogous problem for R2 has already been solved positively (it is known that there are smooth solutions on R2). From the Clay math official problem description:
In two dimensions, the analogues of assertions (A) and (B) have been known for a long time
(Ladyzhenskaya[1]), both for the Navier-Stokes equations and the more difficult Euler equations. This gives no hint
about the three–dimensional case, since the main difficulties are absent in two dimensions.
References
- ^ O. Ladyzhenskaya, The Mathematical Theory of Viscous Incompressible Flows (2nd edition), Gordon and Breach, 1969.
This article contains public-domain material taken from QEDen.
|





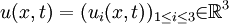 be the unknown velocity vector field, defined for positions
be the unknown velocity vector field, defined for positions 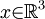 and times
and times 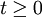 and let
and let 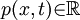 be the unknown
be the unknown 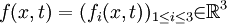 be a known external force, again defined for positions
be a known external force, again defined for positions 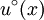 be the known initial velocity vector field on R3, which is divergence-free on C∞.
be the known initial velocity vector field on R3, which is divergence-free on C∞.
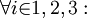
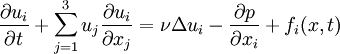
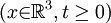
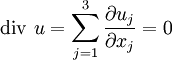
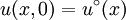
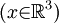
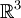
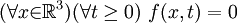
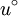 is bounded, i.e.:
is bounded, i.e.:
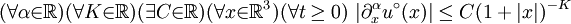
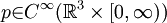 and
and 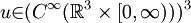 that satisfy (1), (2) and (3) as well as having bounded energy, i.e.:
that satisfy (1), (2) and (3) as well as having bounded energy, i.e.:
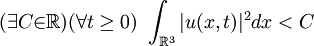
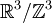
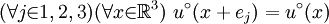 , where
, where 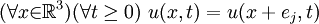
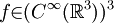 and a divergence-free
and a divergence-free 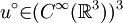 for which there are no
for which there are no 

