To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Optical rotationOptical rotation or optical activity is the rotation of linearly polarized light as it travels through certain materials. It occurs in solutions of chiral molecules such as sucrose (sugar), solids with rotated crystal planes such as quartz, and spin-polarized gases of atoms or molecules. It is used in the sugar industry to measure syrup concentration, in optics to manipulate polarization, in chemistry to characterize substances in solution, and is being developed as a method to measure blood sugar concentration in diabetic people. Product highlight
HistoryThe rotation of the orientation of linearly polarized light was first observed in 1811 in quartz by French physicist Dominique F.J. Arago. Around this same time, Jean Baptiste Biot also observed the effect in liquids and gases of organic substances such as turpentine. In 1822, the English astronomer Sir Joun F.W. Herschel discovered that different crystal forms of quartz rotated the linear polarization in different directions. Simple polarimeters have been used since this time to measure the concentrations of simple sugars, such as glucose, in solution. In fact, one name for glucose, dextrose, refers to the fact that it causes linearly polarized light to rotate to the right or dexter side. Similarly, levulose, more commonly known as fructose, causes the plane of polarization to rotate to the left. Fructose is even more strongly levorotatory than glucose is dextrorotatory. Invert sugar, formed by adding fructose to a solution of glucose, gets its name from the fact that the conversion causes the direction of rotation to "invert" from right to left. In 1849, Louis Pasteur resolved a problem concerning the nature of tartaric acid. A solution of this compound derived from living things (specifically, wine lees) rotated the plane of polarization of light passing through it, but tartaric acid derived by chemical synthesis had no such effect, even though its reactions were identical and its elemental composition was the same. Pasteur noticed that the crystals came in two asymmetric forms that were mirror images of one another. Sorting the crystals by hand gave two forms of the compound: solutions of one form rotated polarized light clockwise, while the other form rotated light counterclockwise. An equal mix of the two had no polarizing effect on light. Pasteur deduced the molecule in question was asymmetric and could exist in two different forms that resemble one another as would left- and right-hand gloves, and that the organic form of the compound consisted purely of the one type. In 1874, Jacobus Henricus van 't Hoff and Joseph Achille Le Bel independently proposed that the phenomenon of optical activity could be explained by assuming that the chemical bonds between carbon atoms and their neighbors were directed towards the corners of a regular tetrahedron. This led to a better understanding of the three-dimensional nature of molecules. TheoryOptical activity is a type of birefringence. Any linear polarization of light can be written as an equal combination of right-hand (RHC) and left-hand circularly (LHC) polarized light: where
This difference is a characteristic of the material (for substances in solution it is given as the specific rotation). After travelling through length L of material the two polarizations pick up a relative phase of
where λ is the wavelength of the light (in vacuum). Consequently, the final polarization is rotated to angle θ0 + Δθ. Generally, the refractive index depends on the wavelength (see dispersion). The variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers-Kronig relations. Complete knowledge of one spectrum allows the calculation of the other. In summary, the degree of rotation depends on the color of the light (the yellow sodium D line near 589 nm wavelength is commonly used for measurements), the path length L and the properties of the material (e.g. Δn or specific rotation and concentration). Areas of use
For a pure substance in solution, if the color and path length are fixed and the specific rotation is known, the observed rotation can be used to calculate the concentration. This usage makes a polarimeter a tool of great importance to those who trade in or use sugar syrups in bulk. In the presence of magnetic fields all molecules have optical activity. A magnetic field aligned in the direction of light propagating through a material will cause the rotation of the plane of linear polarization. This Faraday effect is one of the first discoveries of the relationship between light and electromagnetic effects. Optical activity or rotation should not be confused with circularly polarized light. Circularly polarized light is often presented as a linear polarization rotating as the light propagates. However, in this picture the polarization completely rotates in a length equal to the wavelength (roughly one micrometre) and it can happen in vacuum. In contrast, optical activity only occurs in a material and a complete rotation occurs in a length of millimeters to meters, depending on the material. References
See also
Categories: Polarization | Stereochemistry |
|||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Optical_rotation". A list of authors is available in Wikipedia. | |||||||||||





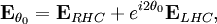
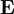 is the electric field of the light. The relative phase between the two
is the electric field of the light. The relative phase between the two 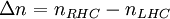 .
.
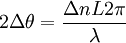 ,
,


