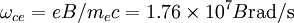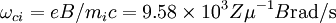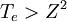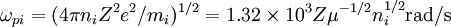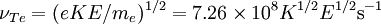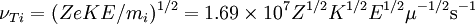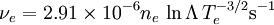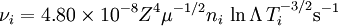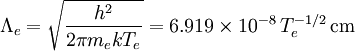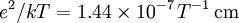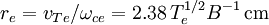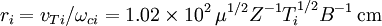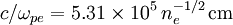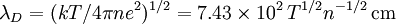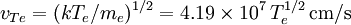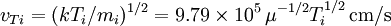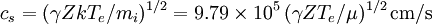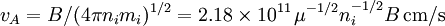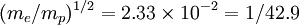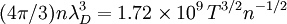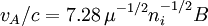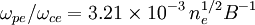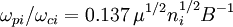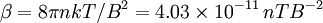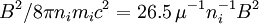My watch list

Plasma parameters

Plasma parameters define various characteristics of a plasma, an electrically conductive collection of charged particles that responds collectively to electromagnetic forces. Plasma typically takes the form of neutral gas-like clouds or charged ion beams, but may also include dust and grains. ^[1] The behaviour of such particle systems can be studied statistically. ^[2]

Additional recommended knowledge

Daily Visual Balance Check

Safe Weighing Range Ensures Accurate Results

What is the Sensitivity of my Balance?

1 Fundamental plasma parameters

Fundamental plasma parameters

All quantities are in Gaussian cgs units except temperature expressed in eV and ion mass expressed in units of the proton mass $μ = m i / m p$ ; Z is charge state; k is Boltzmann's constant; K is wavelength; γ is the adiabatic index; ln Λ is the Coulomb logarithm.

Frequencies

electron gyrofrequency, the angular frequency of the circular motion of an electron in the plane perpendicular to the magnetic field:

$\omega_{ce} = eB/m_ec = 1.76 \times 10^7 B \mbox{rad/s} \,$

ion gyrofrequency, the angular frequency of the circular motion of an ion in the plane perpendicular to the magnetic field:

$\omega_{ci} = eB/m_ic = 9.58 \times 10^3 Z \mu^{-1} B \mbox{rad/s} \,$

electron plasma frequency, the frequency with which electrons oscillate when their charge density is not equal to the ion charge density (plasma oscillation):

$\omega_{pe} = (4\pi n_ee^2/m_e)^{1/2} = 5.64 \times 10^4 n_e^{1/2} \mbox{rad/s}$

ion plasma frequency:

$\omega_{pi} = (4\pi n_iZ^2e^2/m_i)^{1/2} = 1.32 \times 10^3 Z \mu^{-1/2} n_i^{1/2} \mbox{rad/s}$

electron trapping rate

$\nu_{Te} = (eKE/m_e)^{1/2} = 7.26 \times 10^8 K^{1/2} E^{1/2} \mbox{s}^{-1} \,$

ion trapping rate

$\nu_{Ti} = (ZeKE/m_i)^{1/2} = 1.69 \times 10^7 Z^{1/2} K^{1/2} E^{1/2} \mu^{-1/2} \mbox{s}^{-1} \,$

electron collision rate

$\nu_e = 2.91 \times 10^{-6} n_e\,\ln\Lambda\,T_e^{-3/2} \mbox{s}^{-1}$

ion collision rate

$\nu_i = 4.80 \times 10^{-8} Z^4 \mu^{-1/2} n_i\,\ln\Lambda\,T_i^{-3/2} \mbox{s}^{-1}$

Lengths

Electron thermal de Broglie wavelength, approximate average de Broglie wavelength of electrons in a plasma:

$\Lambda_e= \sqrt{\frac{h^2}{2\pi m_ekT_e}}= 6.919\times 10^{-8}\,T_e^{-1/2}\,\mbox{cm}$

classical distance of closest approach, the closest that two particles with the elementary charge come to each other if they approach head-on and each have a velocity typical of the temperature, ignoring quantum-mechanical effects:

$e^2/kT=1.44\times10^{-7}\,T^{-1}\,\mbox{cm}$

electron gyroradius, the radius of the circular motion of an electron in the plane perpendicular to the magnetic field:

$r_e = v_{Te}/\omega_{ce} = 2.38\,T_e^{1/2}B^{-1}\,\mbox{cm}$

ion gyroradius, the radius of the circular motion of an ion in the plane perpendicular to the magnetic field:

$r_i = v_{Ti}/\omega_{ci} = 1.02\times10^2\,\mu^{1/2}Z^{-1}T_i^{1/2}B^{-1}\,\mbox{cm}$

plasma skin depth, the depth in a plasma to which electromagnetic radiation can penetrate:

$c/\omega_{pe} = 5.31\times10^5\,n_e^{-1/2}\,\mbox{cm}$

Debye length, the scale over which electric fields are screened out by a redistribution of the electrons:

$\lambda_D = (kT/4\pi ne^2)^{1/2} = 7.43\times10^2\,T^{1/2}n^{-1/2}\,\mbox{cm}$

Velocities

electron thermal velocity, typical velocity of an electron in a Maxwell-Boltzmann distribution:

$v_{Te} = (kT_e/m_e)^{1/2} = 4.19\times10^7\,T_e^{1/2}\,\mbox{cm/s}$

ion thermal velocity, typical velocity of an ion in a Maxwell-Boltzmann distribution:

$v_{Ti} = (kT_i/m_i)^{1/2} = 9.79\times10^5\,\mu^{-1/2}T_i^{1/2}\,\mbox{cm/s}$

ion sound velocity, the speed of the longitudinal waves resulting from the mass of the ions and the pressure of the electrons:

$c_s = (\gamma ZkT_e/m_i)^{1/2} = 9.79\times10^5\,(\gamma ZT_e/\mu)^{1/2}\,\mbox{cm/s}$

Alfven velocity, the speed of the waves resulting from the mass of the ions and the restoring force of the magnetic field:

$v_A = B/(4\pi n_im_i)^{1/2} = 2.18\times10^{11}\,\mu^{-1/2}n_i^{-1/2}B\,\mbox{cm/s}$

Dimensionless

square root of electron/proton mass ratio

$(m_e/m_p)^{1/2} = 2.33\times10^{-2} = 1/42.9 \,$

number of particles in a Debye sphere

$(4\pi/3)n\lambda_D^3 = 1.72\times10^9\,T^{3/2}n^{-1/2}$

Alven velocity/speed of light

$v_A/c = 7.28\,\mu^{-1/2}n_i^{-1/2}B$

electron plasma/gyrofrequency ratio

$\omega_{pe}/\omega_{ce} = 3.21\times10^{-3}\,n_e^{1/2}B^{-1}$

ion plasma/gyrofrequency ratio

$\omega_{pi}/\omega_{ci} = 0.137\,\mu^{1/2}n_i^{1/2}B^{-1}$

thermal/magnetic pressure ratio ("beta")

$\beta = 8\pi nkT/B^2 = 4.03\times10^{-11}\,nTB^{-2}$

magnetic/ion rest energy ratio

$B^2/8\pi n_im_ic^2 = 26.5\,\mu^{-1}n_i^{-1}B^2$

Category: Plasma physics

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Plasma_parameters". A list of authors is available in Wikipedia.