My watch list

Quantum cascade laser

Quantum cascade lasers (QCLs) are semiconductor lasers that emit in the mid- to far-infrared portion of the electromagnetic spectrum and were first demonstrated by Jerome Faist, Federico Capasso, Deborah Sivco, Carlo Sirtori, Albert Hutchinson, and Alfred Cho at Bell Laboratories in 1994.^[1]

Unlike typical interband semiconductor lasers that emit electromagnetic radiation through the recombination of electron–hole pairs across the material band gap, QCLs are unipolar and laser emission is achieved through the use of intersubband transitions in a repeated stack of semiconductor superlattices, an idea first proposed in the paper "Possibility of amplification of electromagnetic waves in a semiconductor with a superlattice" by R.F. Kazarinov and R.A. Suris in 1971.^[2]

Additional recommended knowledge

Recognize and detect the effects of electrostatic charges on your balance

Safe Weighing Range Ensures Accurate Results

Daily Sensitivity Test

1 Intersubband vs. interband transitions
2 Operating principles
- 2.1 Rate equations
- 2.2 Active region designs
3 Material Systems
4 Emission wavelengths
5 Optical waveguides
6 Growth
7 Applications
8 References

Intersubband vs. interband transitions

Within a bulk semiconductor crystal, electrons may occupy states in one of two continuous energy bands - the valence band, which is heavily populated with low energy electrons and the conduction band, which is sparsely populated with high energy electrons. The two energy bands are separated by an energy band gap in which there are no permitted states available for electrons to occupy. Conventional semiconductor laser diodes generate light by a single photon being emitted when a high energy electron in conduction band recombines with a hole in the valence band. The energy of the photon and hence the emission wavelength of laser diodes is therefore determined by the band gap of the material system used.

A QCL however does not use bulk semiconductor materials in its optically active region. Instead it comprises a periodic series of thin layers of varying material composition forming a superlattice. The superlattice introduces a varying electric potential across the length of the device, meaning that there is a varying probability of electrons occupying different positions over the length of the device. This is referred to as one-dimensional multiple quantum well confinement and leads to the splitting of the band of permitted energies into a number of discrete electronic subbands. By suitable design of the layer thicknesses it is possible to engineer a population inversion between two subbands in the system which is required in order to achieve laser emission. Since the position of the energy levels in the system is primarily determined by the layer thicknesses and not the material, it is possible to tune the emission wavelength of QCLs over a wide range in the same material system.

Additionally, in semiconductor laser diodes, electrons and holes are annihilated after recombining across the band gap and can play no further part in photon generation. However in a unipolar QCL, once an electron has undergone an intersubband transition and emitted a photon in one period of the superlattice, it can tunnel into the next period of the structure where another photon can be emitted. This process of a single electron causing the emission of multiple photons as it traverses through the QCL structure gives rise to the name cascade and makes a quantum efficiency of greater than unity possible which leads to higher output powers than semiconductor laser diodes.

Operating principles

Rate equations

QCLs are typically based upon a three-level system. Assuming the formation of the wavefunctions is a fast process compared to the scattering between states, the time independent solutions to the Schrodinger equation may be applied and the system can be modelled using rate equations. Each subband contains a number of electrons $n i$ (where $i$ is the subband index) which scatter between levels with a lifetime $τ i f$ (reciprocal of the scattering rate $W i f$ ), where $i$ and $f$ are the initial and final subband indices. Assuming that no other subbands are populated, the rate equations for the three laser levels are given by:

$\frac{\mathrm{d}n_3}{\mathrm{d}t} = I_{\mathrm{in}} + \frac{n_1}{\tau_{13}} + \frac{n_2}{\tau_{23}} - \frac{n_3}{\tau_{31}} - \frac{n_3}{\tau_{32}}$

$\frac{\mathrm{d}n_2}{\mathrm{d}t} = \frac{n_3}{\tau_{32}} + \frac{n_1}{\tau_{12}} - \frac{n_2}{\tau_{21}} - \frac{n_2}{\tau_{23}}$

$\frac{\mathrm{d}n_1}{\mathrm{d}t} = \frac{n_2}{\tau_{21}} + \frac{n_3}{\tau_{31}} - \frac{n_1}{\tau_{13}} - \frac{n_1}{\tau_{12}} - I_{\mathrm{out}}$

In the steady state, the time derivatives are equal to zero and $I in = I out = I$ . The general rate equation for electrons in subband i of an N level system is therefore:

$\frac{\mathrm{d}n_i}{\mathrm{d}t} = \sum\limits_{j=1}^N\frac{n_j}{\tau_{ji}}-n_i\sum\limits_{j=1}^N\frac{1}{\tau_{ij}}+I(\delta_{i0}-\delta_{iN})$ ,

Under the assumption that absorption processes can be ignored (which is valid at low temperatures), the middle rate equation gives

$\frac{n_3}{\tau_{32}} = \frac{n_2}{\tau_{21}}$

Therefore if $τ 32 > τ 21$ (i.e. $W 21 > W 32$ ) then $n 3 > n 2$ and a population inversion will exist. The population ratio is defined as

$\frac{n_3}{n_2} = \frac{\tau_{32}}{\tau_{21}} = \frac{W_{21}}{W_{32}}$

If all N steady-state rate equations are summed, the right hand side becomes zero, meaning that the system is underdetermined, and it is possible only to find the relative population of each subband. An additional equation is required to set the total number of carriers equal to the total number of dopant ions:

$\sum\limits_{i=1}^{N}n_i=N_{\mathrm{2D}}$ .

Active region designs

The scattering rates are tailored by suitable design of the layer thicknesses in the superlattice which determine the electron wave functions of the subbands. The scattering rate between two subbands is heavily dependent upon the overlap of the wave functions and energy spacing between the subbands. The figure shows the wave functions in a three quantum well (3QW) QCL active region and injector.

In order to decrease $W 32$ , the overlap of the upper and lower laser levels is reduced. This is often achieved through designing the layer thicknesses such that the upper laser level is mostly localised in the left-hand well of the 3QW active region, while the lower laser level wave function is made to mostly reside in the central and right-hand wells. This is known as a diagonal transition. A vertical transition is one in which the upper laser level is localised in mainly the central and right-hand wells. This increases the overlap and hence $W 32$ which reduces the population inversion, but it increases the strength of the radiative transition and therefore the gain.

In order to increase $W 21$ , the lower laser level and the ground level wave functions are designed such that they have a good overlap and to increase $W 21$ further, the energy spacing between the subbands is designed such that it is equal to the longitudinal optical (LO) phonon energy (~36 meV in GaAs) so that resonant LO phonon-electron scattering can quickly depopulate the lower laser level.

Material Systems

The first QCL was fabricated in the InGaAs/InAlAs material system lattice-matched to an InP substrate.^{[citation needed]} This particular material system has a conduction band offset (quantum well depth) of 520 meV.^{[citation needed]} These InP-based devices have reached very high levels of performance across the mid-infrared spectral range, achieving high power, above room-temperature, continuous wave emission.^{[citation needed]}

In 1998 GaAs/AlGaAs QCLs were demonstrated by Sirtori et al proving that the QC concept is not restricted to one material system.^{[citation needed]} This material system has a varying quantum well depth depending on the aluminium fraction in the barriers.^{[citation needed]} Although GaAs-based QCLs have not matched the performance levels of InP-based QCLs in the mid-infrared, they have proven to be very successful in the Terahertz region of the spectrum.^{[citation needed]}

The short wavelength limit of QCLs is determined by the depth of the quantum well and recently QCLs have been developed in material systems with very deep quantum wells in order to achieve short wavelength emission. The InGaAs/AlAsSb material system has quantum wells 1.6 eV deep and has been used to fabricate QCLs emitting at 3 μm.^{[citation needed]} InAs/AlSb QCLs have quantum wells 2.1 eV deep and electroluminescence at wavelengths as short as 2.5 μm has been observed.^{[citation needed]}

QCLs may also allow laser operation in materials traditionally considered to have poor optical properties. Indirect bandgap materials such as silicon have minimum electron and hole energies at different momentum values. For interband optical transitions, carriers change momentum through a slow, intermediate scattering process, dramatically reducing the optical emission intensity. Intersubband optical transitions however, are independent of the relative momentum of conduction band and valence band minima and theoretical proposals for Si/SiGe quantum cascade emitters have been made.^[3]

Emission wavelengths

QCLs currently cover the wavelength range from 2.7 - 250 μm (and extends to 355 μm with the application of a magnetic field).^{[citation needed]}

Optical waveguides

The linewidth of QCLs is narrowed by incorporating a waveguide into the design, thus amplifying one particular wavelength. Often a structure called a Distributed Bragg reflector (DBR) is built on top of the laser crystal to prevent it from emitting at other than the desired wavelength. Distributed Bragg reflector lasers, characterized by the DBR being outside of the gain medium, should not be confused with distributed feedback (DFB) lasers where the DBR is incorporated into the gain medium.

Growth

The alternating layers of the two different semiconductors which form the quantum heterostructure are grown on to a substrate using molecular beam epitaxy (MBE) or metalorganic vapour phase epitaxy (MOVPE).

Applications

The laser's high optical power output, tuning range and room temperature operation make it useful for spectroscopic applications like the remote sensing of environmental gases and pollutants in the atmosphere. It may eventually be used for vehicular cruise control in conditions of poor visibility, collision avoidance radar, industrial process control, and medical diagnostics such as breath analyzers. QCLs are also being used to study plasma chemistry.

The 3 - 5 μm atmospheric window is also coverable by QCLs paving the way for high-speed, free-space optical communication links which could prove useful for providing high-speed internet access in built up areas as expensive optical fibre installation can be avoided.

Quantum cascade lasers were first commercialized in 2004^[4].

References

^ Faist, Jerome; Federico Capasso, Deborah L. Sivco, Carlo Sirtori, Albert L. Hutchinson, and Alfred Y. Cho (April 1994). "Quantum Cascade Laser". Science 264 (5158): 553-556. doi:10.1126/science.264.5158.553. Retrieved on 2007-02-18.
^ Kazarinov, R.F; Suris, R.A. (April 1971). "Possibility of amplification of electromagnetic waves in a semiconductor with a superlattice". Fizika i Tekhnika Poluprovodnikov 5 (4): 797-800.
^ Paul, Douglas J (2004). "Si/SiGe heterostructures: from material and physics to devices and circuits". Semicond. Sci. Technol. 19: R75-R108. doi:10.1088/0268-1242/19/10/R02. Retrieved on 2007-02-18.
^ Alpes offers CW and pulsed quantum cascade lasers. Laser Focus World. PennWell Publications (2004-04-19). Retrieved on 2007-12-01.

Categories: Semiconductor lasers | Terahertz technology

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Quantum_cascade_laser". A list of authors is available in Wikipedia.
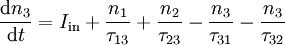
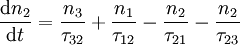
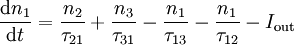
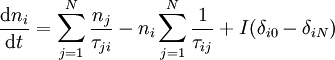
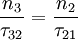
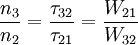
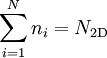