To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Reactions on surfacesBy reactions on surfaces it is understood reactions in which at least one of the steps of the reaction mechanism is the adsorption of one or more reactants. The mechanisms for these reactions, and the rate equations are of extreme importance for heterogeneous catalysis Product highlight
Simple decompositionIf a reaction occurs through these steps: A + S ⇌ AS → Products Where A is the reactant and S is an adsorption site on the surface. If the rate constants for the adsorption, desorption and reaction are k1, k-1 and k2 then, the global reaction rate is: where CAS is the concentration of occupied sites, θ is the surface coverage and CS is the total number of sites (occupied or not). CS is highly related to the total surface area of the adsorbent: the bigger the surface area, the more sites and the faster the reaction. This is the reason why heterogeneous catalysts are usually chosen to have great surface areas (in the order of hundred m2/gram) If we apply the steady state approximation to AS, then
Bimolecular reactionLangmuir-Hinshelwood mechanismThis mechanism proposes that both molecules adsorb and the adsorbed molecules undergo a bimolecular reaction: A + S ⇌ AS B + S ⇌ BS AS + BS → Products The rate constants are now k1,k − 1,k2,k − 2 and k for adsorption of A, adsorption of B, and reaction. The rate law is: Proceeding as before we get
The rate law is complex and there is no clear order respect to any of the reactants but we can consider different values of the constants, for which it is easy to measure integer orders:
That means that 1 > > K1CA,K2CB, so
In this case K1CA,1 > > K2CB, so
One of the reactants has very high adsorption and the other one doesn't adsorb strongly. K1CA > > 1,K2CB, so
Eley-Rideal mechanismThis mechanism proposes that only one of the molecules adsorbs and the other one reacts with it directly, without adsorbing: A + S ⇌ AS AS + B → Products Constants are k1,k − 1 and k and rate equation is r = kCSθACACB. Applying steady state approximation to AS and proceeding as before (considering the reaction the limiting step once more) we get
ReferencesGraphic models of Eley Rideal and Langmuir Hinshelwood mechanisms German page with mechanisms, rate equation graphics and references Categories: Surface chemistry | Chemical kinetics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Reactions_on_surfaces". A list of authors is available in Wikipedia. |





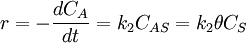
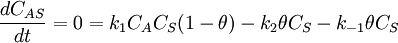 so
so 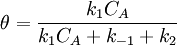 and
and 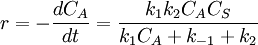 . Please notice that, with
. Please notice that, with 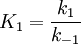 , the formula was divided by
, the formula was divided by 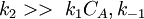 , so
, so 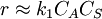 .
The order respect to A is 1. Examples of this mechanism are
.
The order respect to A is 1. Examples of this mechanism are 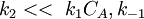 so
so 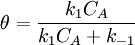 which is just
which is just 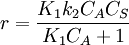 . Depending on the concentration of the reactant the rate changes:
. Depending on the concentration of the reactant the rate changes:
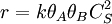
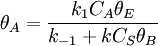 , where
, where 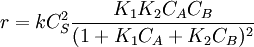 .
.
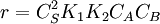 . The order is one respect to both the reactants
. The order is one respect to both the reactants
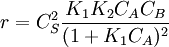 . The reaction order is 1 respect to B. There are two extreme possibilities now:
. The reaction order is 1 respect to B. There are two extreme possibilities now:
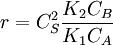 . The order es minus one respect to A. The higher the concentration of A, the slower the reaction goes, in this case we say that A inhibits the reaction.
. The order es minus one respect to A. The higher the concentration of A, the slower the reaction goes, in this case we say that A inhibits the reaction.
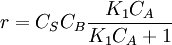 . The order is one respect to B. There are two possibilities, depending on the concetration of reactant A:
. The order is one respect to B. There are two possibilities, depending on the concetration of reactant A:


