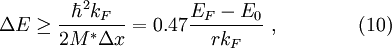To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Scanning tunneling spectroscopyScanning tunneling spectroscopy (STS) is a powerful experimental technique in scanning tunneling microscopy (STM) that uses a scanning tunneling microscope (STM) to probe the local density of electronic states (LDOS) and band gap of surfaces and materials on surfaces at the atomic scale [1]. Generally, STS involves observation of changes in constant-current topographs with tip-sample bias, local measurement of the tunneling current versus tip-sample bias (I-V) curve, measurement of the tunneling conductance, dI / dV, or more than one of these. Since the tunneling current in a scanning tunneling microscope only flows in a region with diameter ~5Å, STS is unique in comparison with other surface spectroscopy techniques, which average over a larger surface region. The origins of STS are found in some of the earliest STM work of Gerd Binnig and Heinrich Rohrer, in which they observed changes in the appearance of some atoms in the (7 x 7) unit cell of the Si(111) – (7 x 7) surface with tip-sample bias [2]. Product highlight
Tunneling CurrentSince STS relies on the tunneling phenomena and measurement of the tunneling current or its derivative, understanding the expressions for the tunneling current is very important. Using the modified Bardeen transfer Hamiltonian method, which treats tunneling as a perturbation, the tunneling current (I) is found to be where describes the energy lowering due to the interaction between the two states. Here ψ and χ are the sample wavefunction modified by the tip potential and the tip wavefunction modified by sample potential, respectively [3]. For low temperatures and a constant tunneling matrix element, the tunneling current reduces to which is a convolution of the DOS of the tip and the sample [3]. Generally, STS experiments attempt to probe the sample DOS, but equation (3) shows that the tip DOS must be known for the measurement to have meaning. Equation (3) implies that under the gross assumption that the tip DOS is constant. For these ideal assumptions, the tunneling conductance is directly proportional to the sample DOS [3]. For higher bias voltages, the predictions of simple planar tunneling models using the Wentzel-Kramers Brillouin (WKB) approximation are useful. In the WKB theory, the tunneling current is predicted to be where ρs and ρt are the density of states (DOS) in the sample and tip, respectively [2]. The energy- and bias-dependent electron tunneling transition probability, T, is given by where φs and φt are the respective work functions of the sample and tip and Z is the distance from the sample to the tip [2]. Experimental MethodsAcquiring standard STM topographs at many different tip-sample biases and comparing the resulting topographic information is perhaps the most straightforward spectroscopic method [4]. The tip-sample bias can also be changed on a line-by-line basis during a single scan. This method creates two interleaved images at different biases [2]. Since only the states between the Fermi levels of the sample and the tip contribute to I, this method is quick way to determine whether there are any interesting bias-dependent features on the surface. However, only limited information about the electronic structure can be extracted by this method, since the constant I topographs depend on the tip and sample DOS’s and the tunneling transmission probability, which depends on the tip-sample spacing, as described in equation (5) [4]. By using modulation techniques, a constant current topograph and the spatially resolved dI / dV can be acquired simultaneously. A small, high frequency sinusoidal modulation voltage is superimposed on the d.c. tip-sample bias. The a.c. component of the tunneling current is recorded using a lock-in amplifier, and the component in-phase with the tip-sample bias modulation gives dI / dV directly. In practice, the modulation frequency is chosen slightly higher than the bandwidth of the STM feedback system [4]. This choice prevents the feedback control from compensating for the modulation by changing the tip-sample spacing and minimizes the displacement current 90° out-of-phase with the applied bias modulation. Such effects arise from the capacitance between the tip and the sample, which grows as the modulation frequency increases [2]. In order to obtain I-V curves simultaneously with a topograph, a sample-and-hold circuit is used in the feedback loop for the z piezo signal. The sample-and-hold circuit freezes the voltage applied to the z piezo, which freezes the tip-sample distance, at the desired location allowing I-V measurements without the feedback system responding [5]. The tip-sample bias is swept between the specified values, and the tunneling current is recorded. After the spectra acquisition, the tip-sample bias is returned to the scanning value, and the scan resumes. Using this method, the local electronic structure of semiconductors in the band gap can be probed [4]. There are two ways to record I-V curves in the manner described above. In constant-spacing scanning tunneling spectroscopy (CS-STS), the tip stops scanning at the desired location to obtain an I-V curve. The tip-sample spacing is adjusted to reach the desired initial current, which may be different from the initial current setpoint, at a specified tip-sample bias. A sample-and-hold amplifier freezes the z piezo feedback signal, which holds the tip-sample spacing constant by preventing the feedback system from changing the bias applied to the z piezo [5]. The tip-sample bias is swept through the specified values, and the tunneling current is recorded. Either numerical differentiation of I(V) or lock-in detection as described above for modulation techniques can be used to find dI / dV. If lock-in detection is used, then an a.c. modulation voltage is applied to the d.c. tip-sample bias during the bias sweep and the a.c. component of the current in-phase with the modulation voltage is recorded. In variable-spacing scanning tunneling spectroscopy (VS-STS), the same steps occur as in CS-STS through turning off the feedback. As the tip-sample bias is swept through the specified values, the tip-sample spacing is decreased continuously as the magnitude of the bias is reduced [7]. Generally, a minimum tip-sample spacing is specified to prevent the tip from crashing into the sample surface at 0V tip-sample bias. Lock-in detection and modulation techniques are used to find the conductivity, because the tunneling current is a function also of the varying tip-sample spacing. Numerical differentiation of I(V) with respect to V would include the contributions from the varying tip-sample spacing [6]. Introduced by Mårtensson and Feenstra to allow conductivity measurements over several orders of magnitude, VS-STS is useful for conductivity measurements on systems with large band gaps. Such measurements are necessary to properly define the band edges and examine the gap for states [7]. Current-imaging-tunneling spectroscopy (CITS) is an STS technique where an I-V curve is recorded at each pixel in the STM topograph [6]. Either variable-spacing or constant-spacing spectroscopy may be used to record the I-V curves. The conductance, dI / dV, can be obtained by numerical differentiation of I with respect to V or acquired using lock-in detection as described above. As a practical concern, the number of pixels in the scan or the scan area may be reduced to prevent piezo creep or thermal drift from moving the feature of study or the scan area during the duration of the scan. Since some CITS scans can last in excess of 12 hours, low drift and creep are absolutely necessary. Data InterpretationFrom the obtained I-V curves, the band gap of the sample at the location of the I-V measurement can be determined. By plotting the magnitude of I on a log scale versus the tip-sample bias, the band gap can clearly be determined. Although determination of the band gap is possible from a linear plot of the I-V curve, the log scale increases the sensitivity [6]. Alternatively, a plot of the conductance, dI / dV, versus the tip-sample bias, V, allows one to locate the band edges that determine the band gap. The structure in the dI / dV, as a function of the tip-sample bias, is associated with the DOS of the surface when the tip-sample bias is less than the work functions of the tip and the sample. Usually, the WKB approximation for the tunneling current is used to interpret these measurements at low tip-sample bias relative to the tip and sample work functions. The derivative of equation (5), I in the WKB approximation, is where ρs is the sample density of states, ρt is the tip density of states, and T is the tunneling transmission probability [2]. Although the tunneling transmission probability T is generally unknown, at a fixed location T increases smoothly and monotonically with the tip-sample bias in the WKB approximation. Hence, structure in the dI / dV is usually assigned to features in the density of states in the first term of equation (7) [4]. Interpretation of dI / dV as a function of position is more complicated. Spatial variations in T show up in measurements of dI / dV as an inverted topographic background. When obtained in constant current mode, images of the spatial variation of dI / dV contain a convolution of topographic and electronic structure. An additional complication arises since dI / dV = I / V in the low-bias limit. Thus, dI / dV diverges as V approaches 0, preventing investigation of the local electronic structure near the Fermi level [4]. Since both the tunneling current, equation (5), and the conductance, equation (7), depend on the tip DOS and the tunneling transition probability, T, quantitative information about the sample DOS is very difficult to obtain. Additionally, the voltage dependence of T, which is usually unknown, can vary with position due to local fluctuations in the electronic structure of the surface [2]. For some cases, normalizing dI / dV by dividing by I / V can minimize the effect of the voltage dependence of T and the influence of the tip-sample spacing. Using the WKB approximation, equations (5) and (7), we obtain [8]: Feenstra et al. argued that the dependencies of where LimitationsWhile STS can provide spectroscopic information with amazing spatial resolution, there are some limitations. The STM and STS lack chemical sensitivity. Since the tip-sample bias range in tunneling experiments is limited to The shape of the tip is of critical importance for the spatial resolution of an STM scan and for the reliability of STS information. The tip density of states always affects information obtained by STS since the spectra are a convolution of the electronic structure of the tip and the sample [2]. In order to obtain an atomic-resolution topographic image, the tip needs to be very sharp. Unfortunately, atomically sharp tips can have prominent, non-uniform electronic structure and produce very unreliable spectroscopy. Very blunt tips with poor spatial resolution are more likely to produce reliable spectroscopy [4]. Feenstra et al. developed an in-situ tip treatment process to produce tips with flatter density of states and free-electron metal behavior. The process uses field emission current to locally heat the end of the tip, leading to local melting and recrystalization that forms facets with low surface energy. For the tungsten (W) tips used, the result of this process is a tip with surface DOS similar to those of a free-electron metal. This process produced tips giving reproducible tunneling spectra [3]. At finite temperatures, the thermal broadening of the electron energy distribution due to the Fermi-distribution limits spectroscopic resolution. At T = 300K, where EF is the Fermi energy, E0 is the bottom of the valence band, kF is the Fermi wave vector, and r is the lateral resolution. Since spatial resolution depends on the tip-sample spacing, smaller tip-sample spacings and higher topographic resolution blur the features in tunneling spectra [3]. Despite these limitations, STS and STM provide the possibility for probing the local electronic structure of metals, semiconductors, and thin insulators on a scale unobtainable with other spectroscopic methods. Additionally, topographic and spectroscopic data can be recorded simultaneously. References
Literature
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Scanning_tunneling_spectroscopy". A list of authors is available in Wikipedia. |





![I=\frac{4\pi e}{\hbar}\int_{-\infty}^{\infty}\left[f\left(E_F-eV+\epsilon\right)-f\left(E_F+\epsilon\right)\right]\rho_S\left(e_F-eV+\epsilon\right)\rho_T\left(E_F+\epsilon\right)\left|M_{\mu\nu}\right|^2\,d\epsilon \ ,\qquad\qquad (1)](images/math/b/9/b/b9bf58eb55f806d7350d0e804f2255ba.png)
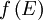 is the
is the 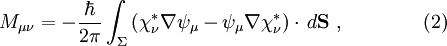
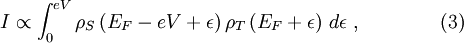
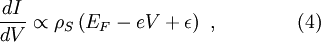
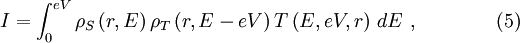
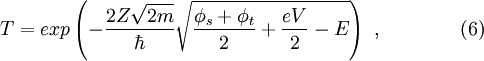
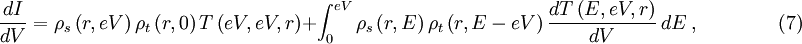
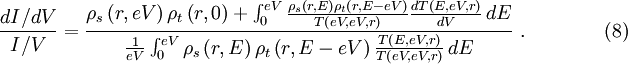
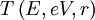 and
and 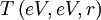 on tip-sample spacing and tip-sample bias tend to cancel, since they appear as ratios [9]. This cancellation reduces the normalized conductance to the following form:
on tip-sample spacing and tip-sample bias tend to cancel, since they appear as ratios [9]. This cancellation reduces the normalized conductance to the following form:
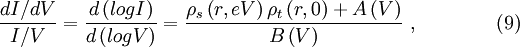
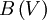 normalizes T to the DOS and
normalizes T to the DOS and 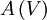 describes the influence of the electric field in the tunneling gap on the decay length. Under the assumption that
describes the influence of the electric field in the tunneling gap on the decay length. Under the assumption that 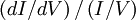 reflect the sample DOS,
reflect the sample DOS, 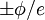 , where
, where 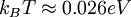 , and the sample and tip energy distribution spread are both
, and the sample and tip energy distribution spread are both 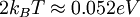 . Hence, the total energy deviation is
. Hence, the total energy deviation is 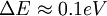 [3]. Assuming the dispersion relation for simple metals, it follows from the uncertainty relation
[3]. Assuming the dispersion relation for simple metals, it follows from the uncertainty relation 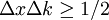 that
that