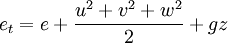To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Shock capturing methodsIn computational fluid dynamics, shock-capturing methods are a class of techniques for computing inviscid flows with shock waves. Computation of flow through shock waves is an extremely difficult task because such flows results in sharp, discontinuous changes in flow variables pressure, temperature, density, and velocity across the shock. Product highlight
ExplanationIn shock-capturing approach the governing equations of inviscid flows (Euler equations) are cast in conservation form and any shock waves or discontinuities are computed as part of the solution. Here, no special treatment is employed to take care of the shocks themselves. This is in contrast to the shock-fitting method, where shock waves are explicitly introduced in the solution using appropriate shock relations (Rankine-Hugoniot relations). The shock capturing methods are relatively simple compared to the more elaborate shock fitting methods. However, the shock waves predicted by shock-capturing methods are generally not sharp and smear over several grid points. Also, classical shock-capturing methods have the disadvantages that unphysical oscillations (Gibbs phenomenon) may develop in the vicinity of strong shocks. Euler equationThe Euler equations are the governing equations for inviscid flows. To implement shock-capturing methods, the conservation form of the Euler equations are used. For a flow without external heat transfer and work transfer (isoenergetic flow), the conservation form of the Euler equation in Cartesian coordinate system can be written as where the vectors U, F, G, and H are given by where et is the total energy (internal energy + kinetic energy + potential energy) per unit mass. That is The Euler equation may be integrated with any of the shock-capturing methods available to obtain the solution. Classical and modern shock capturing methodsFrom an historical point of view, shock-capturing methods can be classified into two general categories: viz., classical methods and modern shock capturing methods (also called high-resolution schemes). Modern shock-capturing methods are generally upwind based in contrast to classical symmetric or central discretization. Upwind-type differencing schemes attempt to discretize hyperbolic partial differential equations by using differencing biased in the direction determined by the sign of the characteristic speeds. On the other hand, symmetric or central schemes do not consider any information about the wave propagation in the discretization. No matter what type of shock-capturing scheme is used, a stable calculation in presence of shock waves requires a certain amount of numerical dissipation, in order to avoid the formation of unphysical numerical oscillations. In the case of classical shock-capturing methods, numerical dissipation terms are usually linear and the same amount is uniformly applied at all grid points. Classical shock-capturing methods only exhibit accurate results in the case of smooth and weak-shock solution, but when strong shock waves are present in the solution, non-linear instabilities and oscillations can arise across discontinuities. Modern shock-capturing methods have, however, a non-linear numerical dissipation, with an automatic feedback mechanism which adjusts the amount of dissipation in any cell of the mesh, in accord to the gradients in the solution. These schemes have proven to be stable and accurate even for problems containing strong shock waves. Some of the well known classical shock-capturing methods include the MacCormack method, Lax-Wendroff method, and Beam-Warming method. Examples of modern shock-capturing schemes include, higher order Total Variation Diminishing (TVD) schemes first proposed by Harten, Flux-Corrected Transport scheme introduced by Boris and Book, Monotonic Upstream-centered Schemes for Conservation Laws (MUSCL) based on Godunov approach and introduced by van Leer, various Essentially Non-Oscillatory schemes (ENO) proposed by Harten et al., and Piecewise Parabolic Method (PPM) proposed by Woodward and Colella. Another important class of high resolution schemes belongs to the approximate Riemann solvers proposed by Roe and by Osher. The schemes proposed by Jameson and Baker, where linear numerical dissipation terms depend on non-linear switch functions, fall in between the classical and modern shock-capturing methods. ReferencesBooks
Technical Papers
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Shock_capturing_methods". A list of authors is available in Wikipedia. |





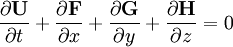
![{\bold U} = \left[ \begin{array}{c} \rho \\ \rho u \\ \rho v \\ \rho w \\ \rho e_t \\ \end{array} \right] \qquad \quad {\bold F} = \left[ \begin{array}{c} \rho u\\ \rho u^2 + p \\ \rho uv \\ \rho uw \\ (\rho e_t + p)u \\ \end{array} \right] \qquad \quad {\bold G} = \left[ \begin{array}{c} \rho v\\ \rho vu \\ \rho v^2 + p \\ \rho vw \\ (\rho e_t + p)v \\ \end{array} \right] \qquad \quad {\bold H} = \left[ \begin{array}{c} \rho w\\ \rho wu \\ \rho wv \\ \rho w^2 + p \\ (\rho e_t + p)w \\ \end{array} \right] \qquad \qquad](images/math/0/c/d/0cdabb3529dfe4ceb7ecd99ef61e8b33.png)