To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Sinusoidal plane-wave solutions of the electromagnetic wave equationPerhaps the most useful solutions to the electromagnetic wave equation are sinusoidal plane-wave solutions. The general solution of the electromagnetic wave equation can be written as a linear superposition of plane-waves of different frequencies and polarizations. Experimentally, every light signal can be decomposed into a spectrum of frequencies and wavelengths associated with sinusoidal solutions of the wave equation. Polarizing filters can be used to decompose light into its various polarization components. The polarization components can be linear, circular or elliptical. The treatment in this article is classical. It is a testament, however, to the generality of Maxwell's equations for electrodynamics that the treatment can be made to be quantum mechanical with only a reinterpretation of classical quantities. The reinterpretation is based on the experiments of Max Planck and the interpretations of those experiments by Albert Einstein. The quantum generalization of the classical treatment can be found in the articles on Photon polarization and Photon dynamics in the double-slit experiment. Product highlight
Plane wavesThe plane sinusoidal solution for an electromagnetic wave traveling in the z direction is (cgs units and SI units) for the electric field and for the magnetic field, where k is the wavenumber, is the angular frequency of the wave, and c is the speed of light. The hats on the vectors indicate unit vectors in the x, y, and z directions. The plane wave is parameterized by the amplitudes and phases where
and
Polarization state vector
Jones vectorAll the polarization information can be reduced to a single vector, called the Jones vector, in the x-y plane. This vector, while arising from a purely classical treatment of polarization, can be interpreted as a quantum state vector. The connection with quantum mechanics is made in the article on photon polarization. The vector emerges from the plane-wave solution. The electric field solution can be re-written in complex notation as where is the Jones vector in the x-y plane. The notation for this vector is the bra-ket notation of Dirac, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector. Dual Jones vectorThe Jones vector has a dual given by
Normalization of the Jones vectorThe Jones vector is normalized. The inner product of the vector with itself is
Polarization statesLinear polarizationIn general, the wave is linearly polarized when the phase angles
This represents a wave polarized at an angle θ with respect to the x axis. In that case the Jones vector can be written
Circular polarizationIf αy is rotated by π / 2 radians with respect to αx the wave is circularly polarized. The Jones vector is where the plus sign indicates right circular polarization and the minus sign indicates left circular polarization. In the case of circular polarization, the electric field vector of constant magnitude rotates in the x-y plane. If unit vectors are defined such that and then a circular polarization state can written in the "R-L basis" as where and
Any arbitrary state can be written in the R-L basis where
Elliptical polarizationThe general case in which the electric field rotates in the x-y plane and has variable magnitude is called elliptical polarization. The state vector is given by
References
See also
Categories: Polarization | Electromagnetic radiation |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Sinusoidal_plane-wave_solutions_of_the_electromagnetic_wave_equation". A list of authors is available in Wikipedia. |





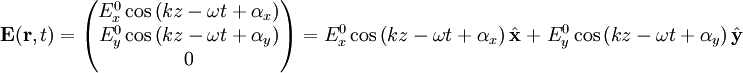
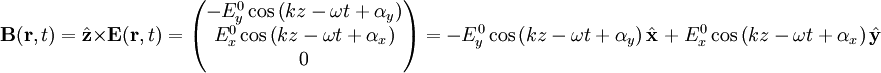
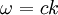
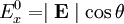
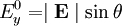
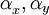
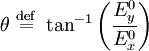 .
.
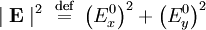 .
.
![\mathbf{E} ( \mathbf{r} , t ) = \mid \mathbf{E} \mid \mathrm{Re} \left \{ |\psi\rangle \exp \left [ i \left ( kz-\omega t \right ) \right ] \right \}](images/math/f/0/7/f07592ed67ae0ecb6ebb466182fcfbde.png)
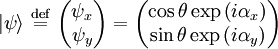
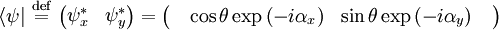 .
.
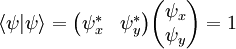 .
.
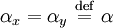 .
.
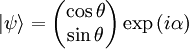 .
.
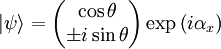
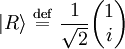
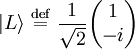
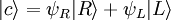
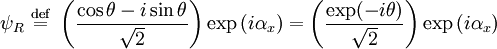
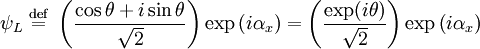 .
.
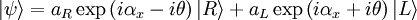
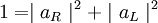 .
.


