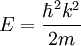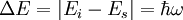To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Surface phononPhonons are collective lattice vibration modes, and surface phonons are those particular modes associated with surfaces; they are an artifact of periodicity, symmetry, and the termination of bulk crystal structure associated with the surface layer of a solid [1]. The study of surface phonons provides valuable insight into the surface structure and other properties specific to the surface region, which often differ from bulk. The figure below gives a pictoral representation of the atomic motion in a phonon mode.
Product highlight
Surface phononsSurface phonons are represented by a wave vector along the surface, q, and an energy corresponding to a particular vibrational mode frequency, ω [1]. The surface Brillouin zone (SBZ) for phonons consists of two dimensions, rather than three for bulk. For example, the face centered cubic (100) surface is described by the directions ΓX and ΓM, referring to the [110] direction and [100] direction, respectively [2]. To describe the displacements of the atoms, one can look at the motions using the Harmonic approximation, in which it is assumed that the force on an atom is a function of its displacement with respect to neighboring atoms, i.e. Hooke’s law holds [3]. Higher order anharmonicity terms are not accounted for in this approximation. To properly account for this, perturbations to this assumption or new descriptions such as proposed by Morse [4] are necessary, but the mathematics becomes far more involved [3]. The positions are then given by the relation
where i is the place where the atom would sit if it were in equilibrium, mi is the mass of the atom that should sit at i, α is the direction of its displacement, ui,α is the amount of displacement of the atom from i, and φiα,jβ are the force constants which come from the crystal potential [1]. The solution to this gives the atomic displacement due to the phonon, which is given by where the atomic position i is described by l, m, and κ, which represent the specific atomic layer, l, the particular unit cell it is in, m, and the position of the atom with respect to its own unit cell, κ [1]. The term x(l,m) is the position of the unit cell with respect to some chosen origin [1]. Phonons can be labeled by the manner in which the vibrations occur. If the vibration occurs lengthwise in the direction of the wave and involves contraction and relaxation of the lattice, the phonon is called a “longitudinal phonon.” Alternatively, the atoms may vibrate side-to-side, perpendicular to wave propagation direction; this is known as a “transverse phonon.” In general, transverse vibrations tend to have smaller frequencies than longitudinal vibrations [3]. The wavelength of the vibration also lends itself to a second label. “Acoustic” branch phonons have a wavelength of vibration that is much bigger than the atomic separation so that the wave travels in the same manner as a sound wave; “optical” phonons can be excited by optical radiation in the infrared wavelength or longer [3]. Phonons take on both labels such that transverse acoustic and optical phonons are denoted TA and TO, respectively; likewise, longitudinal acoustic and optical phonons are denoted LA and LO. Types of surface phononsThe type of surface phonon can be characterized by its dispersion in relation to the bulk phonon modes of the crystal [1]. Surface phonon mode branches may occur in specific parts of the SBZ or encompass it entirely across [1]. These modes can show up both in the bulk phonon dispersion bands as what is known as a resonance or outside these bands as a pure surface phonon mode [5]. Thus surface phonons can be purely surface existing vibrations, or simply the expression of bulk vibrations in the presence of a surface, known as a surface-excess property [2]. A particular mode, the Rayleigh phonon mode, exists across the entire BZ and is known by special characteristics, including a linear frequency versus wave number relation near the SBZ center [1]. Why study surface phononsKnowledge of surface phonon dispersion gives important information related to the amount of surface relaxation, the existence and distance between an adsorbate and the surface, and information regarding presence, quantity, and type of defect existing on the surface [1]. Phonons can couple with electrons and affect the electrical and optical properties of devices, particularly of research interest for the semiconductor Quantum dot [7]. The decreasing size of CdSe quantum dots was found to result in increasing surface phonon frequency, which can couple with electrons and affect their properties [7]. Two useful methods for conceptualizing and modeling surface phonons are the “slab method,” which approaches the problem using lattice dynamics for a solid with parallel surfaces [2], and another method which involves using Green’s function. Which of these approaches is employed is based upon what type of information is required from the computation. For broad surface phonon phenomena, the conventional lattice dynamics method can be used [5]. For information particular to lattice defects, resonances, or phonon state density, the Green’s function method yields more useful results [5]. ExperimentTwo of the more common methods for studying surface phonons are Electron Energy Loss Spectroscopy and Helium Atom Scattering. Electron energy loss spectroscopyThe technique of Electron Energy Loss Spectroscopy (EELS) is based upon the fact that electron energy decreases upon interaction with matter [6]. Since the interaction of low energy electrons is mainly in the surface, the loss is due to surface phonon scattering, which have an energy range of 10-3 eV to 1 eV [6]. In EELS, an electron of known energy is incident upon the crystal, a phonon of some wave number, q, and frequency, ω, is then created, and the outgoing electron’s energy and wave number are measured [1]. If the incident electron energy, Ei, and wave number, ki, are chosen for the experiment and the scattered electron energy, Es, and wave number, ks, are known by measurement, as well as the angles with respect to the normal for the incident and scattered electrons, θi and θs, then values of q throughout the BZ can be obtained [1]. Energy and momentum for the electron have the following relation, where m is the mass of an electron. Energy and momentum must be conserved, so the following relations must be true of the energy and momentum exchange throughout the encounter:
where G is a reciprocal lattice vector that ensures that q falls in the first BZ and the angles θi and θs are measured with respect to the normal to the surface [5]. The dispersion is often shown with q given in units of cm-1, in which 100 cm-1 = 12.41 eV [6]. The electron incident angles for most EELS phonon study chambers can range from 135-θs and 90-θf for θf ranging between 55-65° [5]. Helium atom scatteringHelium is the best suited atom to be used for surface scattering techniques, as it has a low enough mass that multiple phonon scattering events are unlikely, and its closed valence electron shell makes it inert, unlikely to bond with the surface upon which it impinges [5]. In particular, 4He is used because this isotope allows for very precise velocity control, important for obtaining maximum resolution in the experiment [5]. There are two main techniques used for He atom scattering studies. One is a so-called time-of-flight measurement which consists of sending pulses of He atoms at the crystal surface and then measuring the scattered atoms after the pulse [5]. The He beam velocity ranges from 644-2037 m/s [5]. The other involves measuring the momentum of the scattered He atoms by a LiF grating monochromator [5]. It is important to note that the He nozzle beam source used in many He scattering experiments poses some risk of error, as it adds components to the velocity distributions that can mimic phonon peaks; particularly in time-of-flight measurements, these peaks can look very much like inelastic phonon peaks [5]. Thus, these false peaks have come to be known by the names “deceptons” or “phonions” [5]. Comparison of techniquesEELS and Helium scattering techniques each have their own particular merits that warrant the use of either depending on the sample type, resolution desired, etc. Helium scattering has a higher resolution than EELS, with a resolution of 0.5-1 meV compared to 7 meV [5]. However, He scattering is available only for energy differences, Ei-Es, of less than about 30 meV, while EELS can be used for up to 500 meV [5]. During He scattering, the He atom does not actually penetrate into the material, being scattered only once at the surface; in EELS, the electron can go as deep as a few monolayers, scattering more than once during the course of the interaction [5]. Thus, the resulting data is easier to understand and analyze for He atom scattering than for EELS, since there are no multiple collisions to account for. He beams have a capabilities of delivering a beam of higher flux than electrons in EELS, but the detection of electrons is easier than the detection of He atoms [5]. He scattering is also more sensitive to very low frequency vibrations, on the order of 1 meV [5]. This is the reason for its high resolution in comparison to EELS. References[1] J. Szeftel, “Surface phonon dispersion, using electron energy loss spectroscopy,” Surface Science, 152/153 (1985) 797-810. [2] F. W. de Wette “Study of surface phonons by the slab method” W. Kress, F. W. de Wette (eds), Surface Phonons, Springer-Verlag, Berlin Heidelberg (1991). [3] P. Brüesch Phonons: Theory and Experiments I: Lattice Dynamics and Models of Interatomic Forces, Springer-Verlag, Berlin Heidelberg (1982). [4] P. M. Morse Physical Review 34, 57 (1929). [5] J. P. Toennies, “Experimental determination of surface phonons by helium atom and electron energy loss spectroscopy” W. Kress, F. W. de Wette (eds), Surface Phonons, Springer-Verlag, Berlin Heidelberg (1991). [6] K. Oura, V. G. Lifshits, A. A. Saranin, A. V. Zotov, M. Katayama, Surface Science: An Introduction, Springer-Verlag, Berlin Heidelberg (2003). [7] Y.-N. Hwang, S.-H. Park, "Size-dependent surface phonon mode of CdSe quantum dots" Physical Review B 59, 11 (1999) 7285-7288. |
|||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Surface_phonon". A list of authors is available in Wikipedia. |
- Havardia_albicans
- Bosch_reaction
- Shirley_Corriher
- Demonstrating Feshbach resonances between a single ion and ultracold atoms - Researchers study the interaction between lithium atoms and barium ion isolated in ultrahigh vacuum and trapped using light traps
- NIST gets the dirt on soil with 3 new reference materials





![u_{l,m, \kappa , \alpha} = \sqrt{(m_\kappa )} v_{l, \kappa , \alpha } (\omega , q) e^{i[\omega t - q x (l,m)]}](images/math/8/8/f/88ffa55fa91d32b99007341e0408d1c0.png)