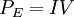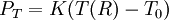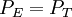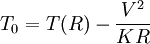To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Thermistor
A thermistor is a type of resistor used to measure temperature changes, relying on the change in its resistance with changing temperature. The word is a combination of thermal and resistor. Samuel Ruben invented the thermistor in 1930, and was awarded U.S. Patent No. 2,021,491. Assuming, as a first-order approximation, that the relationship between resistance and temperature is linear, then:
where
Thermistors can be classified into two types depending on the sign of k. If k is positive, the resistance increases with increasing temperature, and the device is called a positive temperature coefficient (PTC) thermistor, or posistor. If k is negative, the resistance decreases with increasing temperature, and the device is called a negative temperature coefficient (NTC) thermistor. Resistors that are not thermistors are designed to have the smallest possible k, so that their resistance remains nearly constant over a wide temperature range. Thermistors differ from resistance temperature detectors in that the material used in a thermistor is generally a ceramic or polymer, while RTDs use pure metals. The temperature response is also different; RTDs are useful over larger temperature ranges. Product highlight
Steinhart-Hart equationIn practice, the linear approximation (above) works only over a small temperature range. For accurate temperature measurements, the resistance/temperature curve of the device must be described in more detail. The Steinhart-Hart equation is a widely used third-order approximation: where a, b and c are called the Steinhart-Hart parameters, and must be specified for each device. T is the temperature in kelvins and R is the resistance in ohms. To give resistance as a function of temperature, the above can be rearranged into: where
The error in the Steinhart-Hart equation is generally less than 0.02°C in the measurement of temperature. As an example, typical values for a thermistor with a resistance of 3000 Ω at room temperature (25°C = 298.15 K) are: B parameter equationNTC thermistors can also be characterised with the B parameter equation, which is essentially the Steinhart Hart equation with c=0. where the temperatures are in kelvin. Using the expansion only to the first order yields: or or where
Conduction modelMany NTC thermistors are made from a pressed disc or cast chip of a semiconductor such as a sintered metal oxide. They work because raising the temperature of a semiconductor increases the number of electrons able to move about and carry charge - it promotes them into the conducting band. The more charge carriers that are available, the more current a material can conduct. This is described in the formula: I = electric current (ampere)
The current is measured using an ammeter. Over large changes in temperature, calibration is necessary. Over small changes in temperature, if the right semiconductor is used, the resistance of the material is linearly proportional to the temperature. There are many different semiconducting thermistors sizes ranging from about 0.01 kelvin to 2,000 kelvins (-273.14°C to 1,700°C). Most PTC thermistors are of the "switching" type, which means that their resistance rises suddenly at a certain critical temperature. The devices are made of a doped polycrystalline ceramic containing barium titanate (BaTiO3) and other compounds. The dielectric constant of this ferroelectric material varies with temperature. Below the Curie point temperature, the high dielectric constant prevents the formation of potential barriers between the crystal grains, leading to a low resistance. In this region the device has a small negative temperature coefficient. At the Curie point temperature, the dielectric constant drops sufficiently to allow the formation of potential barriers at the grain boundaries, and the resistance increases sharply. At even higher temperatures, the material reverts to NTC behaviour. The equations used for modeling this behaviour were derived by W. Heywang and G. H. Jonker in the 1960s. Another type of PTC thermistor is the polymer PTC, which is sold under brand names such as "Polyfuse", "Polyswitch" and "Multiswitch". This consists of a slice of plastic with carbon grains embedded in it. When the plastic is cool, the carbon grains are all in contact with each other, forming a conductive path through the device. When the plastic heats up, it expands, forcing the carbon grains apart, and causing the resistance of the device to rise rapidly. Like the BaTiO3 thermistor, this device has a highly nonlinear resistance/temperature response and is used for switching, not for proportional temperature measurement. Yet another type of thermistor is a Silistor, a thermally sensitive silicon resistor. Silistors are similarly constructed and operate on the same principles as other thermistors, but employ silicon as the semiconductive component material. Self-heating effectsWhen a current flows through a thermistor, it will generate heat which will raise the temperature of the thermistor above that of its environment. If the thermistor is being used to measure the temperature of the environment, this self-heating effect will introduce an error if a correction is not made. Alternatively, this effect can be employed. It can, for example, make a sensitive air-flow device employed in a sailplane rate-of-climb instrument, the electronic variometer, or serve as a timer for a relay as was formerly done in telephone exchanges. The electrical power input to the thermistor is just where I is current and V is the voltage drop across the thermistor. This power is converted to heat, and this heat energy is transferred to the surrounding environment. The rate of transfer is well described by Newton's law of cooling: where T(R) is the temperature of the thermistor as a function of its resistance R, T0 is the temperature of the surroundings, and K is the dissipation constant, usually expressed in units of milliwatts per °C. At equilibrium, the two rates must be equal. The current and voltage across the thermistor will depend on the particular circuit configuration. As a simple example, if the voltage across the thermistor is held fixed, then by Ohm's Law we have I = V / R and the equilibrium equation can be solved for the ambient temperature as a function of the measured resistance of the thermistor: The dissipation constant is a measure of the thermal connection of the thermistor to its surroundings. It is generally given for the thermistor in still air, and in well-stirred oil. Typical values for a small glass bead thermistor are 1.5 mW/°C in still air and 6.0 mW/°C in stirred oil. If the temperature of the environment is known beforehand, then a thermistor may be used to measure the value of the dissipation constant. For example, the thermistor may be used as a flow rate sensor, since the dissipation constant increases with the rate of flow of a fluid past the thermistor. Applications
References
Manufacturers
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Thermistor". A list of authors is available in Wikipedia. |





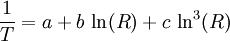
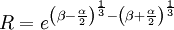
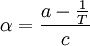 and
and 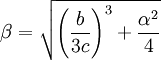
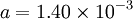
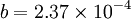
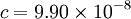
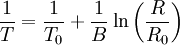
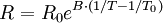
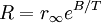
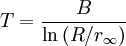
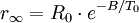
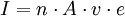
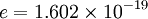 coulomb)
coulomb)