To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Tunable diode laser absorption spectroscopy
Sometimes TDLAS may refer to tunable diode laser atomic absorption spectroscopy, a technique used in plasma diagnostic. Here the TDLAS technique is used for measurement of metastable atom densities or neutral atom temperature and for identification of small amounts of impurities in plasmas. It is, also, possible to correlate the metastable atom densities with the partial pressure of a particularly gas in various gases mixture plasma. The main benefit of this method compared to optical emission methods is the exclusion of spectral lines enlargement due to optical instruments used, because, this width is much smaller than Doppler width – it is about the same order as natural width (about 1 MHz). Product highlight
WorkingTDLAS is a simple technique. A basic TDLAS setup consists of tunable diode laser light source, transmitting (i.e. beam shaping) optics, optically accessible absorbing medium, receiving optics and detector/s. The emission wavelength of the tunable diode laser, viz. VCSEL, DFB, etc., is tuned over the characteristic absorption lines of a species in the gas in the path of the laser beam. This causes a reduction of the measured signal intensity, which can be detected by a photodiode, and then used to determine the gas concentration and other properties as described later. Different diode lasers are used based on the application and the range over which tuning is to be performed. Typical examples are InGaAsP/InP (tunable over 900 nm to 1.6 µm), InGaAsP/InAsP (tunable over 1.6 µm to 2.2 µm), etc. These lasers can be tuned by either adjusting their temperature or by changing injection current density into the gain medium. While temperature changes allow tuning over ~100 cm − 1, it is limited by slow tuninng rates ~few Hz, due to the thermal inertia of the system. On the other hand, adjusting the injection current can provide tuning at rates as high as ~10 GHz, but it is restricted to a smaller range ( ~1 - 2 cm − 1) over which the tuning can be performed. The typical laser linewidth is of the order of 10 − 3 cm − 1 or smaller. Basic PrinciplesConcentration MeasurementThe basic principle behind the TDLAS technique is simple. The focus here is on a single absorption line in the absorption spectrum of the a particular species of interest. To start with the wavelength of a diode laser is tuned over a particular absorption line of interest and the intensity of the transmitted radiation is measured. The transmitted intensity can be related to the concentration of the species present by the Beer-Lambert law, which states that when a radiation of wavenumber where,
Temperature MeasurementThe above relation requires that the temperature where,
Another way to measure the temperature is by relating the FWHM of the probed absorption line to the Doppler line width of the species at that temperature. This is given by, where,
Note: In the last expression, Velocity MeasurementThe effect of a mean flow of the gas in the path of the laser beam can been seen as a shift in the absorption spectrum, also known as Doppler shift. The shift in the frequency spectrum is related to the mean flow velocity by, where,
Note : ApplicationsSee also |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Tunable_diode_laser_absorption_spectroscopy". A list of authors is available in Wikipedia. |





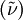 passes through an absorbing medium, the intensity variation along the path of the beam is given by,
passes through an absorbing medium, the intensity variation along the path of the beam is given by,
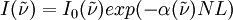
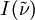 is the transmitted intensity of the radiation after it has traversed a distance
is the transmitted intensity of the radiation after it has traversed a distance 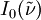 is the initial intensity of the radiation,
is the initial intensity of the radiation,
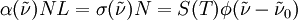 is the absorbance of the medium,
is the absorbance of the medium,
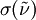 is the absorption cross-section of the absorbing species,
is the absorption cross-section of the absorbing species,
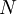 is the number density of the absorbing species,
is the number density of the absorbing species,
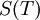 is the line strength (i.e. the total absorption per molecule) of the absorbing species at temperature
is the line strength (i.e. the total absorption per molecule) of the absorbing species at temperature 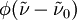 is the lineshape function for the particular absorption line. Sometimes also represented by
is the lineshape function for the particular absorption line. Sometimes also represented by 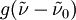 ,
,
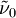 is the center frequency of the spectrum.
is the center frequency of the spectrum.
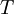 of the absorbing species is known. However, it is possible to overcome this difficulty and measure the temperature simultaneously. There are number of ways to measure the temperature, a widely applied method, which can measure the temperature simultaneously, uses the fact that the line strength
of the absorbing species is known. However, it is possible to overcome this difficulty and measure the temperature simultaneously. There are number of ways to measure the temperature, a widely applied method, which can measure the temperature simultaneously, uses the fact that the line strength ![R =\left( \frac{S_{1}}{S_{2}}\right)_{T} = \left(\frac{S_{1}}{S_{2}} \right)_{T_0} exp\left[-\frac{hc(E_{1}-E_{2})}{k}\left(\frac{1}{T}-\frac{1}{T_{0}} \right) \right]](images/math/4/c/5/4c579e0df9a3aacdcdad65ec67f6d471.png)
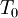 is some reference temperature at which the line strengths are known,
is some reference temperature at which the line strengths are known,
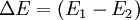 is the difference in the lower
is the difference in the lower 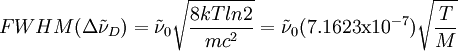
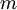 is the weight of one molecule of the species, and
is the weight of one molecule of the species, and
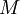 is the
is the 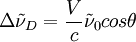
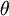 is the angle between the flow direction and the laser beam direction.
is the angle between the flow direction and the laser beam direction.
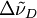 is not same as the one mentioned before where it refers to the width of the spectrum. The shift is usually very small (~
is not same as the one mentioned before where it refers to the width of the spectrum. The shift is usually very small (~

