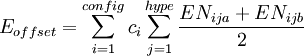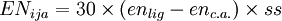To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
VALBONDIn molecular mechanics, VALBOND is a method for computing the angle bending energy that is based on valence bond theory.[1] It is based on orbital strength functions, which are maximized when the hybrid orbitals on the atom are orthogonal. The hybridization of the bonding orbitals are obtained from empirical formulas based on Bent's rule, which relates the preference towards p character with electronegativity. The VALBOND functions are suitable for describing the energy of bond angle distortion not only around the equilibrium angles, but also at very large distortions. This represents an advantage over the simpler harmonic oscillator approximation used by many force fields, and allows the VALBOND method to handle hypervalent molecules[2] and transition metal complexes.[3],[4] The VALBOND energy term has been combined with force fields such as CHARMM and UFF to provide a complete functional form that includes also bond stretching, torsions, and non-bonded interactions. Product highlight
Functional formNon-hypervalent moleculesFor an angle α between normal (non-hypervalent) bonds involving an spmdn hybrid orbital, the energy contribution is
where k is an empirical scaling factor that depends on the elements involved in the bond, Smax, the maximum strength function, is and S(α) is the strength function which depends on the nonorthogonality integral Δ: The energy contribution is added twice, once per each of the bonding orbitals involved in the angle (which may have different hybridizations and different values for k). For non-hypervalent p-block atoms, the hybridization value n is zero (no d-orbital contribution), and m is obtained as %p(1-%p), where %p is the p character of the orbital obtained from where the sum over j includes all ligands, lone pairs, and radicals on the atom, np is the "gross hybridization" (for example, for an "sp2" atom, np = 2). The weight wti depends on the two elements involved in the bond (or just one for lone pair or radicals), and represents the preference for p character of different elements. The values of the weights are empirical, but can be rationalized in terms of Bent's rule. Hypervalent moleculesFor hypervalent molecules, the energy is represented as a combination of VALBOND configurations, which are akin to resonance structures that place three-center four-electron bonds (3c4e) in different ways. For example, ClF3 is represented as having one "normal" two-center bond and one 3c4e bond. There are three different configurations for ClF3, each one using a different Cl-F bond as the two-center bond. For more complicated systems the number of combinations increases rapidly; SF6 has 45 configurations.
where the sum is over all configurations j, and the coefficient cj is defined by the function where "hype" refers to the 3c4e bonds. This function ensures that the configurations where the 3c4e bonds are linear are favored. The energy terms are modified by multiplying them by a bond order factor, BOF, which is the product of the formal bond orders of the two bonds involved in the angle (for 3c4e bonds, the bond order is 0.5). For 3c4e bonds, the energy is calculated as where Δ is again the non-orthogonality function, but here the angle α is offset by 180 degrees (π radians). Finally, to ensure that the axial vs equatorial preference of different ligands in hypervalent compounds is reproduced, an "offset energy" term is subtracted. It has the form where the EN terms depend on the electronegativity difference between the ligand and the central atom as follows: where ss is 1 if the electronegativity difference is positive and 2 if it is negative. For p-block hypervalent molecules, d orbitals are not used, so n = 0. The p contribution m is estimated from ab initio quantum chemistry methods and a natural bond orbital (NBO) analysis. References
|
|||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "VALBOND". A list of authors is available in Wikipedia. |





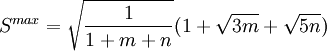
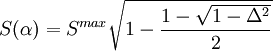
![\Delta = \frac{1}{1+m+n} \left [ 1+m \cos \alpha + \frac{n}{2}(3 \cos ^2 \alpha -1) \right ]](images/math/7/6/0/760fb8e6b5afd22b3c4564fc61103b93.png)
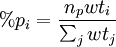
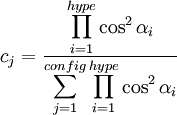
![E(\alpha) = BOF \times k_{\alpha} [1-\Delta(\alpha + \pi)^2]](images/math/d/a/7/da796c2dbc85a84b4a849b0ed0683814.png)