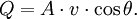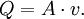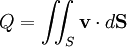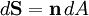To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Volumetric flow rateIn fluid dynamics and hydrometry, the volumetric flow rate, also volume flow rate and rate of fluid flow, is the volume of fluid which passes through a given surface per unit time (for example cubic meters per second [m3 s-1] in SI units, or cubic feet per second [cu ft/s]). It is usually represented by the symbol Q. Volumetric flow rate should not be confused with volumetric flux, represented by the symbol q, with units of m3/(m2 s), that is, m s-1. The integration of a flux over an area gives the volumetric flow rate. Volumetric flow rate is also linked to viscosity. Product highlightGiven an area A, and a fluid flowing through it with uniform velocity v with an angle θ away from the perpendicular to A, the flow rate is: In the special case where the flow is perpendicular to the area A, that is, θ = 0, the volumetric flow rate is: If the velocity of the fluid through the area is non-uniform (or if the area is non-planar) then the rate of fluid flow can be calculated by means of a surface integral: where dS is a differential surface described by: with n the unit surface normal and dA the differential magnitude of the area. If a surface S encloses a volume V, the divergence theorem states that the rate of fluid flow through the surface is the integral of the divergence of the velocity vector field v on that volume:
See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Volumetric_flow_rate". A list of authors is available in Wikipedia. |