To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle (usually, an electron) placed in a periodic potential. It consists of the product of a plane wave envelope function and a periodic function (periodic Bloch function) Product highlightThe result that the eigenfunctions can be written in this form for a periodic system is called Bloch's theorem. The corresponding energy eigenvalue is Єn(k)= Єn(k + K), periodic with periodicity K of a reciprocal lattice vector. Because the energies associated with the index n vary continuously with wavevector k we speak of an energy band with band index n. Because the eigenvalues for given n are periodic in k, all distinct values of Єn(k) occur for k-values within the first Brillouin zone of the reciprocal lattice. More generally, a Bloch-wave description applies to any wave-like phenomenon in a periodic medium. For example, a periodic dielectric in electromagnetism leads to photonic crystals, and a periodic acoustic medium leads to phononic crystals. It is generally treated in the different forms of the dynamical theory of diffraction. The plane wave wavevector (or Bloch wavevector) k (multiplied by the reduced Planck's constant, this is the particle's crystal momentum) is unique only up to a reciprocal lattice vector, so one only needs to consider the wavevectors inside the first Brillouin zone. For a given wavevector and potential, there are a number of solutions, indexed by n, to Schrödinger's equation for a Bloch electron. These solutions, called bands, are separated in energy by a finite spacing at each k; if there is a separation that extends over all wavevectors, it is called a (complete) band gap. The band structure is the collection of energy eigenstates within the first Brillouin zone. All the properties of electrons in a periodic potential can be calculated from this band structure and the associated wavefunctions, at least within the independent electron approximation. A corollary of this result is that the Bloch wavevector k is a conserved quantity in a crystalline system (modulo addition of reciprocal lattice vectors), and hence the group velocity of the wave is conserved. This means that electrons can propagate without scattering through a crystalline material, almost like free particles, and that electrical resistance in a crystalline conductor only results from things like imperfections that break the periodicity. It can be shown that the eigenfunctions of a particle in a periodic potential can always be chosen this form by proving that translation operators (by lattice vectors) commute with the Hamiltonian. More generally, the consequences of symmetry on the eigenfunctions are described by representation theory. The concept of the Bloch state was developed by Felix Bloch in 1928, to describe the conduction of electrons in crystalline solids. The same underlying mathematics, however, was also discovered independently several times: by George William Hill (1877), Gaston Floquet (1883), and Alexander Lyapunov (1892). As a result, a variety of nomenclatures are common: applied to ordinary differential equations, it is called Floquet theory (or occasionally the Lyapunov-Floquet theorem). Various one-dimensional periodic potential equations have special names, for example, Hill's equation:[1].
where the θ's are constants. Hill's equation is very general, as the θ-related terms may viewed as a Fourier series expansion of a periodic potential. Other much studied periodic one-dimensional equations are the Kronig-Penney model and Mathieu's equation. References
See alsoFurther reading
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Bloch_wave". A list of authors is available in Wikipedia. |


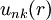 which has the same periodicity as the potential:
which has the same periodicity as the potential:
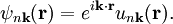



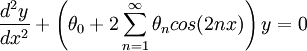 ,
,


