To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Polytropic processA polytropic process is a thermodynamic process that obeys the relation:
where P is pressure, V is volume, n is any real number (the polytropic index), and C is a constant. This equation can be used to accurately characterize processes of certain systems, notably the compression or expansion of a gas, but in some cases, possibly liquids and solids. Under standard conditions, most gases can be accurately characterized by the ideal gas law. This construct allows for the pressure-volume relationship to be defined for essentially all ideal thermodynamic cycles, such as the well-known Carnot cycle. (Note however that there may be instances where a polytropic process occurs in a non-ideal gas.) For certain indices n, the process will be synonymous with other processes:
When the index n occurs between any two of the former values (0,1,gamma, or infinity), it means that the polytropic curve will lie between the curves of the two corresponding indicies. The equation is a valid characterization of a thermodynamic process assuming that:
Additional recommended knowledge
Polytropic fluidsPolytropic fluids are idealized fluid models that are used often in astrophysics. A polytropic fluid is a type of barotropic fluid for which the equation of state is written as: P = Kρ(1 + 1 / n) where P is the pressure, K is a constant, ρ is the density, and n is a quantity called the polytropic index. This is also commonly written in the form: P = Kργ where in this case, γ = (1 + 1 / n) (Note that γ need not be the adiabatic index (the ratio of specific heats), and in fact often it is not. This is sometimes a cause for confusion.) GammaIn the case of an isentropic ideal gas, γ is the ratio of specific heats, known as the adiabatic index. An isothermal ideal gas is also a polytropic gas. Here, the polytropic index is equal to one, and differs from the adiabatic index γ. In order to discriminate between the two gammas, the polytropic gamma is sometimes capitalized, Γ. To confuse matters further, some authors refer to Γ as the polytropic index, rather than n. Note that
OtherA solution to the Lane-Emden equation using a polytropic fluid is known as a polytrope. See also |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Polytropic_process". A list of authors is available in Wikipedia. |


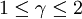 , since
, since 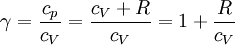 (see:
(see: 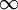 , then it is an
, then it is an