To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Isobaric process
Product highlight
According to the first law of thermodynamics, where W is work done by the system, U is internal energy, and Q is heat. Pressure-volume work (by the system) is defined as: (Δ means change over the whole process, it doesn't mean differential) but since pressure is constant, this means that
Applying the ideal gas law, this becomes assuming that the quantity of gas stays constant (e.g. no phase change during a chemical reaction). Since it is generally true that then substituting the last two equations into the first equation produces:
The quantity in parentheses is equivalent to the molar specific heat for constant pressure:
and if the gas involved in the isobaric process is monatomic then An isobaric process is shown on a P-V diagram as a straight horizontal line, connecting the initial and final thermostatic states. If the process moves towards the right, then it is an expansion. If the process moves towards the left, then it is a compression. Defining EnthalpyAn isochoric process is described by the equation Q = ΔU. It would be convenient to have a similar equation for isobaric processes. Substituting the second equation into the first yields The quantity U + p V is a state function so that it can be given a name. It is called enthalpy, and is denoted as H. Therefore an isobaric process can be more succinctly described as
See also
Categories: Thermodynamic processes | Atmospheric thermodynamics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Isobaric_process". A list of authors is available in Wikipedia. |





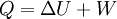
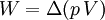
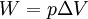 .
.
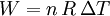
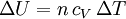
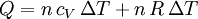
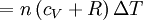 .
.
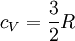 and
and 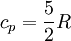 .
.
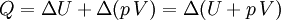
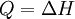 .
.


