To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Born approximationIn scattering theory and, in particular in quantum mechanics, the Born approximation consists of taking the incident field in place of the total field as the driving field at each point in the scatterer. It is the perturbation method applied to scattering by an extended body. It is accurate if the scattered field is small, compared to the incident field, in the scatterer. For example, the radar scattering of radio waves by a light styrofoam column can be approximated by assuming that each part of the plastic is polarized by the same electric field that would be present at that point without the column, and then calculating the scattering as a radiation integral over that polarization distribution. Product highlight
Born approximation to the Lippmann-Schwinger equationThe Lippmann-Schwinger equation for the scattering state where This equation becomes within Born approximation which is much easier to solve since the right hand side does not depend on the unknown state The obtained solution is the starting point of the Born series. Scattering by two potentialsIn its simplest form, the incident and scattered waves and the Born approximation Other applications include bremsstrahlung and the Photoelectric effect. For charged particle induced direct nuclear reaction, the procedure is used twice. There are similar methods that do not use Born approximations. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Born_approximation". A list of authors is available in Wikipedia. |





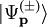 with a momentum p and out-going (+) or in-going (-) boundary conditions is
with a momentum p and out-going (+) or in-going (-) boundary conditions is
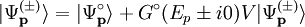
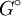 is the free particle
is the free particle 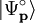 is the corresponding free scattering solution sometimes called incident field. The factor
is the corresponding free scattering solution sometimes called incident field. The factor 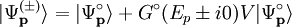
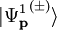 to a part
to a part