To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Boussinesq approximation (buoyancy)In fluid dynamics, the Boussinesq approximation (named for Joseph Valentin Boussinesq) is used in the field of buoyancy-driven flow. It states that density differences are sufficiently small to be neglected, except where they appear in terms multiplied by g, the acceleration due to gravity. The essence of the Boussinesq approximation is that the difference in inertia is negligible but gravity is sufficiently strong to make the specific weight appreciably different between the two fluids. Sound waves are impossible/neglected when the Boussinesq approximation is used since sound waves move via density variations. Product highlightBoussinesq flows are common in nature (such as atmospheric fronts, oceanic circulation, katabatic winds), industry (dense gas dispersion, fume cupboard ventilation), and the built environment (natural ventilation, central heating). The approximation is extremely accurate for many such flows, and makes the mathematics and physics simpler. The approximation's advantage arises because when considering a flow of, say, warm and cold water of density ρ1 and ρ2 one needs only consider a single density ρ: the difference Δρ = ρ1 − ρ2 is negligible. Dimensional analysis shows that, under these circumstances, the only sensible way that acceleration due to gravity g should enter into the equations of motion is in the reduced gravity g' where
(Note that the denominator may be either density without affecting the result because the change would be of order g(Δρ / ρ)2). The most generally used dimensionless number would be the Richardson number. The mathematics of the flow is therefore simpler because the density ratio (ρ1 / ρ2, a dimensionless number) does not affect the flow; the Boussinesq approximation states that it may be assumed to be exactly one. InversionsOne feature of Boussinesq flows is that they look the same when viewed upside-down, provided that the identities of the fluids are reversed. The Boussinesq approximation is inaccurate when the nondimensionalised density difference Δρ / ρ is of order unity. For example, consider an open window in a warm room. The warm air inside is lighter than the cold air outside, which flows into the room and down towards the floor. Now imagine the opposite: a cold room exposed to warm outside air. Here the air flowing in moves up toward the ceiling. If the flow is Boussinesq (and the room is otherwise symmetrical), then viewing the cold room upside down is exactly the same as viewing the warm room right-way-round. This is because the only way density enters the problem is via the reduced gravity g' which undergoes only a sign change when changing from the warm room flow to the cold room flow. An example of a non-Boussinesq flow is bubbles rising in water. The behaviour of air bubbles rising in water is very different from the behaviour of water falling in air: in the former case rising bubbles tend to form hemispherical shells, while water falling in air splits into raindrops (at small length scales surface tension enters the problem and confuses the issue). |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Boussinesq_approximation_(buoyancy)". A list of authors is available in Wikipedia. |





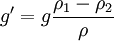 .
.


