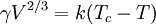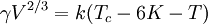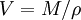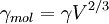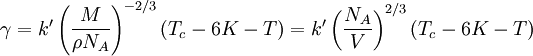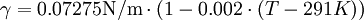Eötvös rule

The Eötvös rule, named after the Hungarian physicist Loránd (Roland) Eötvös (1848-1919) enables the prediction of the surface tension of an arbitrary liquid pure substance at all temperatures. The density, molar mass and the critical temperature of the liquid have to be known. At the critical point the surface tension is zero.

The first assumption of the Eötvös rule is:

1. The surface tension is a linear function of the temperature.

This assumption is approximately fulfilled for most known liquids. When plotting the surface tension versus the temperature a fairly straight line can be seen which has a surface tension of zero at the critical temperature.

The Eötvös rule also gives a relation of the surface tension behaviour of different liquids in respect to each other:

2. The temperature dependence of the surface tension can be plotted for all liquids in a way that the data collapses to a single master curve. To do so either the molar mass, the density, or the molar volume of the corresponding liquid has to be known.

Additional recommended knowledge

What is the Sensitivity of my Balance?

How to quickly check pipettes?

Daily Sensitivity Test

The Eötvös rule

If V is the molar volume and T_c the critical temperature of a liquid the surface tension γ is given by^[1]

where k is a constant valid for all liquids. The Eötvös constant has a value of 2.1×10⁻⁷ J/K mol^−2/3.

More precise values can be gained when considering that the line normally passes the temperature axis 6 K before the critical point:

The molar volume V is given by the molar mass M and the density ρ

The term γV^{2 / 3} is also referred to as the "molar surface tension" γ_mol :

A useful representation that prevents the use of the unit mol^−2/3 is given by the Avogadro constant N_A :

As John Lennard-Jones and Corner showed in 1940 by means of the statistical mechanics the constant k' is nearly equal to the Boltzmann constant.

Water

For water following equation applies

Historical

As student Eötvös started to research surface tension and developed a new method for its determination. The Eötvös rule was first found phenomenological and published in 1886. In 1893 William Ramsay and Shields showed an improved version considering that the line normally passes the temperature axis 6 K before the critical point. John Lennard-Jones and Corner published (1940) a derivation of the equation by means of statistical mechanics. In 1945 E. A. Guggenheim gave a further improved variant of the equation.

References

1. ^ Surface Tension by the Ring Method (Du Nouy Method) (pdf). PHYWE. Retrieved on 2007-09-08.