To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Fiber Bragg gratingA fiber Bragg grating (FBG) is a type of distributed Bragg reflector constructed in a short segment of optical fiber that reflects particular wavelengths of light and transmits all others. This is achieved by adding a periodic variation to the refractive index of the fiber core, which generates a wavelength specific dielectric mirror. A fiber Bragg grating can therefore be used as an inline optical filter to block certain wavelengths, or as a wavelength-specific reflector. Product highlight
HistoryThe first in-fiber Bragg grating was demonstrated by Hill in 1978.[1] Initially, the gratings were fabricated using a visible laser propagating along the fiber core. In 1989, Meltz and colleagues demonstrated the modern transverse holographic technique from the side of the fiber utilizing the interference pattern of ultraviolet light.[2] ManufactureFiber Bragg gratings are created by "inscribing" or "writing" the periodic variation of refractive index into the core of an optical fiber using an intense ultraviolet (UV) source such as a UV laser. Two main processes are used: interference and masking. Which is best depends on the type of grating to be manufactured. A special germanium-doped silica fiber is used in the manufacture of fiber Bragg gratings. The germanium-doped fiber is photosensitive; where the refractive index of the core changes with exposure to UV light, with the amount of change depending on the exposure intensity and duration. InterferenceThe first manufacturing method, specifically used for uniform gratings, is the use of two-beam interference. Here the UV laser is split into two beams which interfere with each other creating a periodic intensity distribution along the interference pattern. The refractive index of the photosensitive fiber changes according to the intensity of light that it is exposed to. This method allows for quick and easy changes to the Bragg wavelength, which is a directly related to the interference period, which is a function of the incident angle of the laser light. PhotomaskA photomask having the intended grating features may also be used in the manufacture of fiber Bragg gratings. The photomask is placed between the UV light source and the photosensitive fiber. The shadow of the photomask then determines the grating structure based on the transmitted intensity of light striking the fiber. Photomasks are specifically used in the manufacture of chirped Fiber Bragg gratings, which cannot be manufactured using an interference pattern. Point-by-pointA single UV laser beam may also be used to 'write' the grating into the fiber point-by-point. Here, the laser has a narrow beam that is equal to the grating period. This method is specifically applicable to the fabrication of long period fiber gratings. Point-by-point is also used in the fabrication of tilted gratings. ProductionOriginally, the manufacture of the photosensitive optical fiber and the 'writing' of the fiber Bragg grating were done separately. Today, production lines typically draw the fiber from the preform and 'write' the grating, all in a single stage. As well as reducing associated costs and time, this also enables the mass production of fiber Bragg gratings. Mass production is in particular facilitating applications in smart structures utilizing large numbers (3000) of embedded fiber Bragg gratings along a single length of fiber. TheoryThe fundmental principle behind the operation of a FBG, is Fresnel reflection. Where light traveling between media of different refractive indicies may both reflect and refract at the interface. The grating will typically have a sinusoidal refractive index variation over a defined length. The reflected wavelength (λB), called the Bragg wavelength, is defined by the relationship,
where n is the average refractive index of the grating and Λ is the grating period. Referring to Figure 1, n is the average of n2 and n3. The wavelength spacing between the first minimums (nulls), or the bandwidth (Δλ), is given by,
where δn0 is the variation in the refractive index (n3 − n2), and η is the fraction of power in the core. The peak reflection (PB(λB)) is approximately given by,
where N is the number of periodic variations. The full equation for the reflected power (PB(λ)), is given by,
where,
Types of gratingsThe term “type” in this context refers to the underlying photosensitivity mechanism by which grating fringes are produced in the fibre. The different methods of creating these fringes have a significant effect on physical attributes of the produced grating, particularly the temperature response and ability to withstand elevated temperatures. Thus far, four types of FBG have been reported with different underlying photosensitivity mechanisms. These are summarised below: Type I gratings
Type I gratings are usually known as standard gratings and are manufactured in fibres of all types under all hydrogenation conditions. Typically, the reflection spectra of a type I grating is equal to 1-T where T is the transmission spectra. This means that the reflection and transmission spectra are complementary and there is negligible loss of light by reflection into the cladding or by absorption. Type I gratings are the most commonly used of all grating types, and the only types of grating available off-the-shelf at the time of writing. Type IA gratings
Type IA gratings were first published in 2001[3] during experiments designed to determine the effects of hydrogen loading on the formation of IIA gratings in germanosilicate fibre. In contrast to the anticipated blue shift of the peak Bragg wavelength, a large positive wavelength shift was measured. This type IA grating appeared once the conventional type I FBG had reached saturation followed by subsequent complete or partial erasure, and was therefore labelled as regenerated. It was also noted that the temperature coefficient of the regenerated grating was lower than a standard grating written under similar conditions. There is a clear relationship between type IA and IIA gratings insomuch as their fabrication conditions are identical in all but one aspect: they both form in B/Ge co-doped fibre but IAs form only in hydrogenated fibres and IIAs form only in non-hydrogenated fibres.[3][4][5] Type II gratings
Archambault et al showed that it was possible to inscribe gratings of ~100% (>99.8%) reflectance with a single UV pulse in fibres on the draw tower. The resulting gratings were shown to be stable at temperatures as high as 800˚C. The gratings were inscribed using a single 40mJ pulse from an excimer laser at 248nm. It was further shown that a sharp threshold was evident at ~30mJ; above this level the index modulation increased by more than two orders of magnitude, whereas below 30mJ the index modulation grew linearly with pulse energy. For ease of identification, and in recognition of the distinct differences in thermal stability, they labelled gratings fabricated below the threshold as type I gratings and above the threshold as type II gratings. Microscopic examination of these gratings showed a periodic damage track at the grating’s site within the fibre [10]; hence type II gratings are also known as damage gratings. [6][7] Type IIA gratings
Later research by Xie et al showed the existence of another type of grating with similar thermal stability properties to the type II grating. This grating exhibited a negative change in the mean index of the fibre and was termed type IIA. The gratings were formed in germanosilicate fibres with pulses from a frequency doubled XeCl pumped dye laser. It was shown that initial exposure formed a standard (type I) grating within the fibre which underwent a small red shift before being erased. Further exposure showed that a grating reformed which underwent a steady blue shift whilst growing in strength. [8][9] Grating structure
The structure of the FBG can vary via the refractive index, or the grating period. The grating period can uniform or graded, and either localised or distributed in a superstructure. The refractive index has two primary characteristics, the refractive index profile, and the offset. Typically, the refractive index profile can be uniform or apodized, and the refractive index offset is positive or zero. There are six common structures for FBGs;[10]
Apodized gratingsThere are basically two quantities that control the properties of the FBG. These are the grating length, Lg, given as,
and the grating strength, δn0 η. There are, however, three properties that need to be controlled in a FBG. These are the reflectivity, the bandwidth, and the side-lobe strength. From the equation (2) above, we see that the bandwidth depends on the grating strength, and not the grating length. This means the grating strength can be used to set the bandwidth. The grating length, effectively N, can then be used to set the peak reflectivity according to equation (3), which depend on both the grating strength and the grating length. The result of this, is that the side-lobe strength can not be controlled, and this simple optimisation results in significant side-lobes. A third quantity can be varied to help with side-lobe suppression. This is apodization of the refractive index change. The term appodization refers to the grading of the refractive index to approach zero at the end on the grating. Apodized gratings offer significant improvement is side-lobe suppression, while maintain reflectivity, and a narrow bandwidth. The two functions are typically used to apodize a FBG are a Gaussian, and a raised-cosine. Chirped fiber Bragg gratingsThe refractive index profile of the grating may be modified to add other features, such as a linear variation in the grating period, called a chirp. The chirp had the effect of broadening the reflected spectrum. The reflected wavelength, given by equation (1), will change relative to any change in the grating period. A grating possessing a chirp has the property of adding dispersion - namely, different wavelengths reflected from the grating will be subject to different delays. This property has been used in the development of phased-array antenna systems. Tilted fiber Bragg gratingsIn standard FBGs, the grading or variation of the refractive index is along the length of the fiber (the optical axis), and is typically uniform across the width of the fiber. In a tilted FBG (TFBG), the variation of the refractive index is at an angle to the optical axis. The angle of tilt in a TFBG has an effect on the reflected wavelength, and bandwidth. Long-period gratingsTypically the grating period is the same size as the Bragg wavelength, as defined in equation (1). So for a grating that reflects at 1500nm, the grating period is 500nm, using a refractive index of 1.5. Longer periods can be used to achieve much broader responses then are possible with a standard FBG. These gratings are called long-period fiber grating. They typically have grating periods on the order of 100 micrometers, to a millimeter, and are therefore much easier to manufacture. ApplicationsCommunicationsThe primary application of fiber Bragg gratings is in optical communications systems. They are specifically used as notch filters. They are also used in optical multiplexers and demultiplexers with an optical circulator, or Optical Add-Drop Multiplexer (OADM). Figure 5 shows 4 channels, depicted as 4 colours, impinging onto a FBG via an optical circulator. The FBG is set to reflect one of the channels, here channel 4. The signal is reflected back to the circulator where it is directed down and dropped out of the system. Since the channel has been dropped, another signal on that channel can be added at the same point in the network. A demultiplexer can be achieved by cascading multiple drop sections of the OADM, where each drop element uses a FBG set to the wavelength to be demultiplexed. Conversely, a multiplexer can be achieved by cascading multiple add sections of the OADM. FBG demultiplexers and OADMs can also be tunable. In a tunable demultiplexer or OADM, the Bragg wavelength of the FBG can be tuned by strain applied by a piezoelectric transducer. The sensitivity of a FBG to strain is discussed below in fiber Bragg grating sensors. Fiber Bragg grating sensorsAs well as being sensitive to strain, the Bragg wavelength is also sensitive to temperature. This means that fiber Bragg gratings can be used as sensing elements in optical fiber sensors. In a FBG sensor, the measurand causes a shift in the Bragg wavelength, ΔλB. The relative shift in the Bragg wavelength, ΔλB / λB, due to an applied strain (ε) and a change in temperature (ΔT) is approximately given by,
or,
Here, CS is the coefficient of strain, which is related to the strain optic coefficient pe. Also, CT is the coefficient of temperature, which is made up of the thermal expansion coefficient of the optical fiber, αΛ, and the thermo-optic coefficient, αn[11]. Fiber Bragg gratings can then be used as direct sensing elements for strain and temperature. They can also be used as transduction elements, converting the output of another sensor, which generates a strain or temperature change from the measurand, for example fiber Bragg grating gas sensors use an absorbent coating, which in the presence of a gas expands generating a strain, which is measurable by the grating. Technically, the absorbent material is the sensing element, converting the amount of gas to a strain. The Bragg grating then transduces the strain to the change in wavelength. Specifically, fiber Bragg gratings are finding uses in instrumentation applications such as seismology and as downhole sensors in oil and gas wells for measurement of the effects of external pressure, temperature, seismic vibrations and inline flow measurement. As such they offer a significant advantage over traditional electronic gauges used for these applications in that they are less sensitive to vibration or heat and consequently are far more reliable. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fiber_Bragg_grating". A list of authors is available in Wikipedia. |





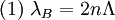 ,
,
![(2) \ \Delta \lambda=\left[\frac{2 \delta n_0 \eta}{\pi}\right]\lambda_B](images/math/6/e/f/6eff3c0346707bd9076116f7f06fc738.png) ,
,
![(3) \ P_B(\lambda_B) \approx \tanh^2 \left[\frac{N \eta (V) \delta n_0}{n}\right]](images/math/d/5/f/d5f55dd5a48abd71aa1b8eebda83be74.png) ,
,
![(4) \ P_B(\lambda) = \frac{\sinh^2\left[ N \eta (V) \delta n_0 \sqrt(1-\Gamma^2) N \Lambda / \lambda\right]}{\cosh^2\left[\eta (V) \delta n_0 \sqrt(1-\Gamma^2) N \Lambda / \lambda\right]-\Gamma^2}](images/math/7/5/1/75152270e54471e841c33dd9437f1485.png) ,
,
![(5) \ \Gamma (\lambda)=\frac{\pi}{\eta (V) \delta n_0}\left[\frac{\lambda}{\lambda_B}-1\right]](images/math/3/1/8/318c683d36eae38e1490b1c9fb34bd64.png) .
.
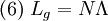 ,
,
![(7) \ \left[\frac{\Delta \lambda_B}{\lambda}\right]= C_S\epsilon + C_T\Delta T](images/math/2/f/3/2f3420ca0bdf552dae07971a952f39d1.png) ,
,
![(8) \ \left[\frac{\Delta \lambda_B}{\lambda}\right]= (1-p_e)\epsilon + (\alpha_\Lambda + \alpha_n)\Delta T](images/math/d/b/0/db0eeb3bdbde6a5bd27510c711d374e7.png) .
.


