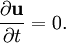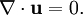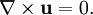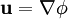To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Flow velocityIn fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of the fluid. Product highlight
DefinitionThe flow velocity of a fluid is a vector field which gives the velocity of an element of fluid at a point UsesThe flow velocity of a fluid effectively describes everything about the motion of a fluid. Many physical properties of a fluid can be expressed mathematically in terms of the flow velocity. Some common examples follow: Steady flowThe flow of a fluid is said to be steady if Incompressible flowA fluid is incompressible if the divergence of That is, if Irrotational flowA flow is irrotational if the curl of That is, if VorticityThe vorticity, ω, of a flow can be defined in terms of its flow velocity by Thus in irrotational flow the vorticity is zero. The velocity potentialIf an irrotational flow occupies a simply-connected fluid region then there exists a scalar field φ such that The scalar field φ is called the velocity potential for the flow. (See Irrotational vector field.) Categories: Fluid dynamics | Fluid mechanics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Flow_velocity". A list of authors is available in Wikipedia. |





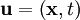
 at a time
at a time  does not vary with time. That is if
does not vary with time. That is if