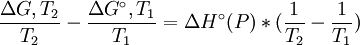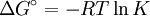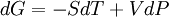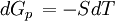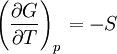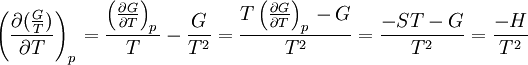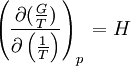To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Gibbs-Helmholtz equationThe Gibbs-Helmholtz equation is a thermodynamic equation useful for calculating changes in the Gibbs energy of a system as a function of temperature. It is named after Josiah Willard Gibbs and Hermann von Helmholtz: Product highlightWith:
at constant pressure For a chemical reaction the equation reads: with which can rearrange to: This equation quickly enables the calculation of the Gibbs free energy change for a chemical reaction at any temperature T2 with knowledge of just the Standard Gibbs free energy change of formation and the Standard enthalpy change of formation for the individual components at 25°C and 1 bar. Through: which relates Gibbs energy to an equilibrium constant, the van 't Hoff equation is derived.
ProofThe Gibbs free energy for a closed system
The dependence of the G/T ratio on T is found with the aid of the quotient rule: From times it can be found like this: |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gibbs-Helmholtz_equation". A list of authors is available in Wikipedia. |


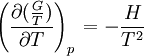



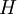 the
the 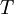 the absolute temperature
the absolute temperature
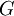 the
the 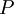 . The equation states that the change in the G/T ratio at constant pressure as a result of an infinitesimally small change in temperature is a factor (H/T2).
. The equation states that the change in the G/T ratio at constant pressure as a result of an infinitesimally small change in temperature is a factor (H/T2).
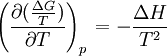
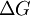 as the change in Gibbs energy and
as the change in Gibbs energy and 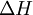 as the enthalpy change (which is considered independent of temperature).
as the enthalpy change (which is considered independent of temperature).