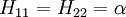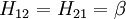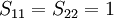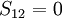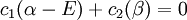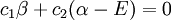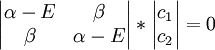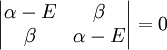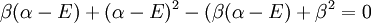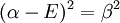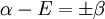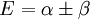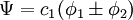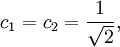The Hückel method or Hückel molecular orbital method (HMO) proposed by Erich Hückel in 1930, is a very simple LCAO MO Method for the determination of energies of molecular orbitals of pi electrons in conjugated hydrocarbon systems, such as ethene, benzene and butadiene. [1] [2] It is the theoretical basis for the Hückel's rule; the extended Hückel method developed by Roald Hoffmann is the basis of the Woodward-Hoffmann rules [3]. It was later extended to conjugated molecules such as pyridine, pyrrole and furan that contain atoms other than carbon, known in this context as heteroatoms. [4]
It is a very powerful educational tool and details appear in many chemistry textbooks.
Hückel characteristics
The method has several characteristics:
- It limits itself to conjugated hydrocarbons
- Only pi electron MO's are included because these determine the general properties of these molecules and the sigma electrons are ignored. This is referred to as sigma-pi separability.
- The method takes as inputs the LCAO MO Method, the Schrödinger equation and simplifications based on orbital symmetry considerations. Interestingly the method does not take in any physical constants.
- The method predicts how many energy levels exist for a given molecule, which levels are degenerate and it expresses the MO energies as the sum of two other energy terms called alpha, the energy of an electron in a 2p-orbital and beta, an interaction energy between two p orbitals which are still unknown but importantly have become independent of the molecule. In addition it enables calculation of charge density for each atom in the pi framework, the bond order between any two atoms and the overall molecular dipole moment.
Hückel results
The results for a few simple molecules are tabulated below:
| Molecule | Energy | Frontier orbital | HOMO - LUMO energy gap
|
| Ethylene | E1 = α - β | LUMO | -2β
|
| E2 = α + β | HOMO |
|
| Butadiene | E1 = α + 1.62β | |
|
| E2 = α + 0.62β | HOMO | -1.24β
|
| E3 = α - 0.62β | LUMO |
|
| E4 = α - 1.62β | |
|
| Benzene | E1 = α + 2β | |
|
| E2 = α + β | |
|
| E3 = α + β | HOMO | -2β
|
| E4 = α - β | LUMO |
|
| E5 = α - β | |
|
| E6 = α - 2β | |
|
| Cyclobutadiene | E1 = α + 2β | |
|
| E2 = α | SOMO | 0
|
| E3 = α | SOMO |
|
| E4 = α - 2β | |
|
| Table 1. Hückel method results Lowest energies op top α and β are both negative values [5]
|
The theory predicts two energy levels for ethylene with its two pi electrons filling the low-energy HOMO and the high energy LUMO remaining empty. In butadiene the 4 pi electrons occupy 2 low energy MO's out of a total of 4 and for benzene 6 energy levels are predicted two of them degenerate.
For linear and cyclic systems (with n atoms), general solutions exist [6].
Linear: 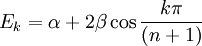
Cyclic: 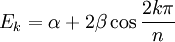
Many predictions have been experimentally verified:
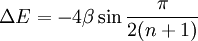
- from which a value for β can be obtained between −60 and −70 kcal/mol (−250 to −290 kJ/mol).[7]
- The predicted MO energies as stipulated by Koopmans' theorem correlate with photoelectron spectroscopy.[8]
- The Hückel delocalization energy correlates with the experimental heat of combustion. This energy is defined as the difference between the total predicted pi energy (in benzene 8β) and a hypothetical pi energy in which all ethylene units are assumed isolated each contributing 2β (making benzene 3 x 2β = 6β).
- Molecules with MO's paired up such that only the sign differs (for example α+/-β) are called alternant hydrocarbons and have in common small molecular dipole moments. This is in contrast to non-alternant hydrocarbons such as azulene and fulvene that have large dipole moments. The Hückel-theory is more accurate for alternate hydrocarbons.
- For cyclobutadiene the theory predicts that the two high-energy electrons occupy a degenerate pair of MO's that are neither stabilized or destabilized. Hence the square molecule would be a very reactive triplet diradical (the ground state is actually rectangular without degenerate orbitals). In fact, all cyclic conjugated hydrocarbons with a total of 4n pi electrons share this MO pattern and this form the basis of Hückel's rule.
Mathematics behind the Hückel Method
The Hückel method can be derived from the Ritz method with a few further assumptions concerning the overlap matrix S and the Hamiltonian matrix H.
It is assumed that the overlap matrix S is the identity Matrix. This means that overlap between the orbitals is neglected and the orbitals are considered orthogonal. Then the generalised eigenvalue problem of the Ritz method turns into an eigenvalue problem.
The Hamiltonian matrix H = (Hij) is parametrised in the following way:
Hii = α for C atoms and α + hA β for other atoms A.
Hij = β if the two atoms are next to each other and both C, and kAB β for other neighbouring atoms A and B.
Hij = 0 in any other case
The orbitals are the eigenvectors and the energies are the eigenvalues of the Hamiltonian matrix. If the substance is a pure hydrocarbon the problem can be solved without any knowledge about the parameters. For heteroatom systems, such as pyridine, values of hA and kAB have to be specified.
Hückel solution for ethylene
In the Hückel treatment for ethylene [9], the molecular orbital 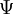 is a linear combination of the 2p atomic orbitals is a linear combination of the 2p atomic orbitals 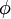 at carbon with their ratio's at carbon with their ratio's 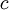 : :
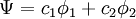
This equation is substituted in the Schrödinger equation:
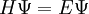
with 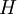 the Hamiltonian and the Hamiltonian and 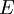 the energy corresponding to the molecular orbital the energy corresponding to the molecular orbital
to give:
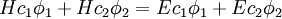
This equation is multiplied by 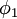 and integrated to give new set of equations: and integrated to give new set of equations:
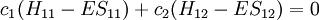
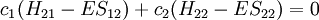
where:
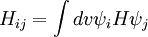
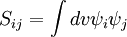
All diagonal Hamiltonian integrals 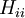 are called coulomb integrals and those of type are called coulomb integrals and those of type 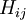 , where atoms i and j are connected, are called resonance integrals with these relationships: , where atoms i and j are connected, are called resonance integrals with these relationships:
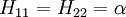
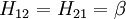
Other assumptions are that the overlap integral between the two atomic orbitals is 0
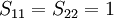
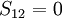
leading to these two homogeneous equations:
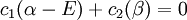
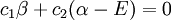
with a total of five variables. After converting this set to matrix notation:
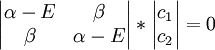
the trivial solution gives both wavefunction coefficients c equal to zero which is not useful so the other (non-trivial) solution is :
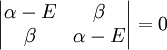
which can be solved by expanding its determinant:
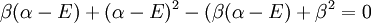
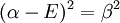
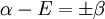
or
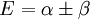
and
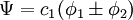
After normalization the coefficients are obtained:
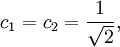
The constant β in the energy term is negative and therefore α + β is the lower energy corresponding to the HOMO and is α - β the LUMO energy.
Further reading
- The HMO-Model and its applications: Basis and Manipulation, E. Heilbronner and H. Bock, English translation, 1976, Verlag Chemie.
- The HMO-Model and its applications: Problems with Solutions, E. Heilbronner and H. Bock, English translation, 1976, Verlag Chemie.
- The HMO-Model and its applications: Tables of Hückel Molecular Orbitals , E. Heilbronner and H. Bock, English translation, 1976, Verlag Chemie.
References
- ^ E. Hückel, Zeitschrift für Physik, 70, 204, (1931); 72, 310, (1931); 76, 628 (1932); 83, 632, (1933)
- ^ Hückel Theory for Organic Chemists, C. A. Coulson, B. O'Leary and R. B. Mallion, Academic Press,1978.
- ^ Stereochemistry of Electrocyclic Reactions R. B. Woodward, Roald Hoffmann J. Am. Chem. Soc.; 1965; 87(2); 395-397. doi:10.1021/ja01080a054
- ^ Andrew Streitwieser, Molecular Orbital Theory for Organic Chemists, Wiley, New York, (1961)
- ^ The chemical bond 2nd Ed. J.N. Murrel, S.F.A. Kettle, J.M. Tedder ISBN 0471907600)
- ^ Quantum Mechanics for Organic Chemists. Zimmmerman, H., Academic Press, New York, 1975.
- ^ Use of Huckel Molecular Orbital Theory in Interpreting the Visible Spectra of Polymethine Dyes: An Undergraduate Physical Chemistry Experiment. Bahnick, Donald A. J. Chem. Educ. 1994, 71, 171.
- ^ Huckel theory and photoelectron spectroscopy. von Nagy-Felsobuki, Ellak I. J. Chem. Educ. 1989, 66, 821.
- ^ Quantum chemistry workbook Jean-Louis Calais ISBN 0471594350
|





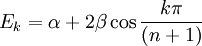
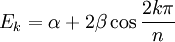
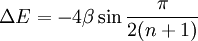
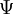 is a linear combination of the 2p
is a linear combination of the 2p 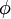 at carbon with their ratio's
at carbon with their ratio's 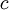 :
:
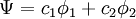
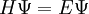
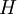 the Hamiltonian and
the Hamiltonian and 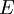 the energy corresponding to the molecular orbital
the energy corresponding to the molecular orbital
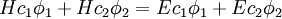
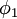 and integrated to give new set of equations:
and integrated to give new set of equations:
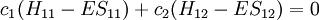
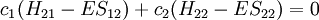
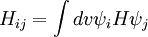
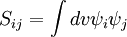
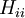 are called coulomb integrals and those of type
are called coulomb integrals and those of type 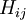 , where atoms i and j are connected, are called resonance integrals with these relationships:
, where atoms i and j are connected, are called resonance integrals with these relationships: