To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hamiltonian fluid mechanicsHamiltonial fluid mechanics is the application of Hamiltonian methods to fluid mechanics. This formalism can only apply to nondissipative fluids. Product highlightTake the simple example of a barotropic, inviscid vorticity-free fluid. Then, the conjugate fields are the density field ρ and the velocity potential φ. The Poisson bracket is given by and the Hamiltonian by where u is the internal energy density. This gives rise to the following two equations of motion: where after exploiting the fact that the vorticity is zero. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hamiltonian_fluid_mechanics". A list of authors is available in Wikipedia. |





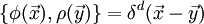
![H=\int d^dx \left[ \frac{1}{2}\rho(\nabla \phi)^2 +u(\rho) \right]](images/math/0/5/8/0587d621f2205df185e3ab964d058ce5.png)
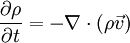
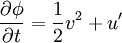
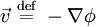 is the velocity and is vorticity-free. The second equation leads to the
is the velocity and is vorticity-free. The second equation leads to the