To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Henderson-Hasselbalch equationIn chemistry, the Henderson-Hasselbalch (frequently misspelled Henderson-Hasselbach) equation describes the derivation of pH as a measure of acidity (using pKa, the acid dissociation constant) in biological and chemical systems. The equation is also useful for estimating the pH of a buffer solution and finding the equilibrium pH in acid-base reactions (it is widely used to calculate isoelectric point of the proteins). Two equivalent forms of the equation are and
In these equations, A − denotes the ionic form of the relevant acid. Bracketed quantities such as [base] and [acid] denote the molar concentration of the quantity enclosed. In analogy to the above equations, the following equation is valid: Where B + denotes the salt of the corresponding base B. Product highlight
HistoryLawrence Joseph Henderson wrote an equation, in 1908, describing the use of carbonic acid as a buffer solution. Karl Albert Hasselbalch later re-expressed that formula in logarithmic terms, resulting in the Henderson-Hasselbalch equation [1]. Hasselbalch was using the formula to study metabolic acidosis, which results from carbonic acid in the blood. LimitationsThere are some significant approximations implicit in the Henderson-Hasselbalch equation. The most significant is the assumption that the concentration of the acid and its conjugate base at equilibrium will remain the same as the formal concentration. This neglects the dissociation of the acid and the hydrolysis of the base. The dissociation of water itself is neglected as well. These approximations will fail when dealing with relatively strong acids or bases (pKa more than a couple units away from 7), dilute or very concentrated solutions (less than 1 mM or greater than 1M), or heavily skewed acid/base ratios (more than 100 to 1). See alsoReferences
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Henderson-Hasselbalch_equation". A list of authors is available in Wikipedia. |


![\textrm{pH} = \textrm{pK}_{a}+ \log_{10} \frac{[\textrm{A}^-]}{[\textrm{HA}]}](images/math/a/b/1/ab1b03e5b89fae2809f9126df0530e8a.png)
![pH = pK_{a}+\log_{10} \left ( \frac{[\mathrm{base}]}{[\mathrm{acid}]} \right ).](images/math/0/f/c/0fc2a150675019257df739b26406eca9.png)
![pK_{a} = - \log_{10}(K_{a}) = - \log_{10} \left ( \frac{[\mbox{H}_{3}\mbox{O}^+][\mbox{A}^-]}{[\mbox{HA}]} \right )](images/math/2/0/8/20845d1b79802fde9f21fd36be129fb2.png) for the non-specific Brønsted acid-base reaction:
for the non-specific Brønsted acid-base reaction: 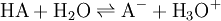
![\textrm{pOH} = \textrm{pK}_{b}+ \log_{10} \frac{[\textrm{BH}^+]}{[\textrm{B}]}](images/math/f/4/7/f47cc68326580d9b2658f69a4f913f9c.png)





