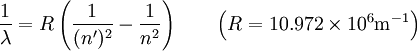Hydrogen spectral series

In physics, the spectral lines of hydrogen correspond to particular jumps of the electron between energy levels. The simplest model of the hydrogen atom is given by the Bohr model. When an electron jumps from a higher energy to a lower, a photon of a specific wavelength is emitted according to the Rydberg formula:

Additional recommended knowledge

What is the Sensitivity of my Balance?

Essential Laboratory Skills Guide

How to quickly check pipettes?

where n is the initial energy level and n' is the final energy level, and R is the Rydberg constant.

The spectral lines are grouped into series according to n' :

Lyman Series			Balmer Series
n	λ(nm)		n	λ(nm)
2	122		3	656
3	103		4	486
4	97.2		5	434
5	94.9		6	410
6	93.7		7	397
	91.1			365

Paschen Series			Brackett Series
n	λ(nm)		n	λ(nm)
4	1870		5	4050
5	1280		6	2630
6	1090		7	2170
7	1000		8	1940
8	954		9	1820
	820			1460

Pfund Series			Humphreys Series
n	λ(nm)		n	λ(nm)
6	7460		7	12372
7	4650		8	7503
8	3740		10	5129
9	3300		11	4673
10	3040		13	4171
	2280			3282

Extension

Hydrogen is the element with the simplest-to-analyze emission spectrum. All other atoms possess at least two electrons in their unionized form and the interactions between these electrons makes analysis of the spectrum by such simple methods as described here impractical. The deduction of the Rydberg formula was a major step in physics, but it was long before an extension to the spectra of other elements could be accomplished.

See also

• Bohr model