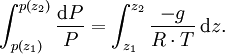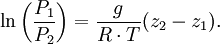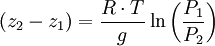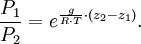To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hypsometric equationThe hypsometric equation relates the atmospheric pressure ratio to the thickness of an atmospheric layer under the assumptions of constant temperature and gravity. It is derived from the hydrostatic equation and the ideal gas law. Product highlightIt is expressed as: where:
In meteorology P1 and P2 are isobaric surfaces and T is the average temperature of the layer between them. In altimetry with the International Standard Atmosphere the hypsometric equation is used to compute pressure at a given geopotential height in isothermal layers in the upper and lower stratosphere. DerivationThe hydrostatic equation: where This is combined with the ideal gas law: to eliminate This is integrated from Integration gives: simplifying to: Rearranging: or, eliminating the logarithm: References
Categories: Fluid mechanics | Temperature | Atmospheric thermodynamics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hypsometric_equation". A list of authors is available in Wikipedia. |





![\ h = z_2 - z_1 = \frac{R \cdot T}{g} \cdot \ln \left [ \frac{P_1}{P_2} \right ]](images/math/f/d/2/fd291c9dac8360c7ea00f1afadc66154.png)
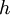 = thickness of the layer [m]
= thickness of the layer [m]
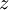 = geopotential height [m]
= geopotential height [m]
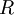 =
= 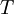 =
= 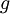 = gravitational acceleration [m/s2]
= gravitational acceleration [m/s2]
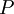 =
= 
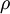 is the
is the 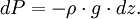

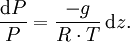
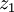 to
to 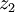 :
: