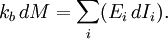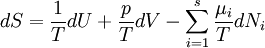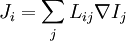To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Non-equilibrium thermodynamics
Product highlight
Basic conceptsThere are many examples of stationary non-equilibrium systems, some very simple, like a system confined between two thermostats at different temperatures or the ordinary Couette flow, a fluid enclosed between two flat walls moving in opposite directions and defining non-equilibrium conditions at the walls. Laser action is also a non-equilibrium thermodynamic process. Here a strong temperature difference is maintained between two molecular degrees of freedom (with molecular laser, vibrational and rotational molecular motion). Damping of acoustical perturbations or shock waves are non-stationary non-equilibrium processes. The mechanics of macroscopic systems depends on a number of extensive quantities. It should be stressed that all systems are permanently interacting with their surroundings, thereby causing unavoidable fluctuations of extensive quantities. Equilibrium conditions of thermodynamic systems are related to the maximum property of the entropy. If the only extensive quantity that is allowed to fluctuate is the internal energy, all the other ones being kept strictly constant, the temperature of the system is measurable and meaningful. The system's properties are then most conveniently described using the thermodynamic potential Helmholtz free energy (A = U - TS), a Legendre transformation of the energy. If, next to fluctuations of the energy, the macroscopic dimensions (volume) of the system are left fluctuating, we use the Gibbs free energy (G = U + PV - TS), where the system's properties are determined both by the temperature and by the pressure. Non-equilibrium systems are much more complex and they may undergo fluctuations of more extensive quantities. The boundaries conditions impose to them particular intensive variables, like temperature gradients or distorted collective motions (shear motions, vortices, etc), often called thermodynamic forces. If free energies are very useful in equilibrium thermodynamics, it must be stressed that there is no general law defining stationary non-equilibrium properties of the energy as is the second law of thermodynamics for the entropy in equilibrium thermodynamics. That is why in such cases a more generalized Legendre transformation should be considered. This is the extended Massieu potential. By definition, the entropy (S) is a function of the collection of extensive quantities Ei. Each extensive quantity has a conjugate intensive variable Ii (a restricted definition of intensive variable is used here by comparison to the definition in given in this link) so that: We then define the extended Massieu function as follows: where The independent variables are the intensities. Intensities are global values, valid for the system as a whole. When boundaries impose to the system different local conditions, (e.g. temperature differences), there are intensive variables representing the average value and others representing gradients or higher moments. The latter are the thermodynamic forces driving fluxes of extensive properties through the system. It may be shown that the Legendre transformation changes the maximum condition of the entropy (valid at equilibrium) in a minimum condition of the extended Massieu function for stationary states, no matter whether at equilibrium or not. Flows and forcesThe fundamental relation of thermodynamics expresses the change in entropy dS of a system as a function of the intensive quantities temperature T, pressure p and ith chemical potential μi and of the differentials of the extensive quantities energy U, volume V and ith particle number Ni. Using U, V and Ni as our basis of the extensive quantities, we then see that the corresponding thermodynamic forces are the gradients of 1 / T, p / T and μi / T respectively. In stationary conditions, the extensive quantities are by definition constant. We may therefore state that the system's entropy is equally constant. However, according to Ilya Prigogine and others , when an open system is allowed to reach a stationary state, it organizes itself so as to minimize total entropy production. In fact, entropy production does not occur within the system but it is located at the boundaries where the system exchanges its extensive properties with the neighbourhood. The intensive variables representing gradients of properties are thermodynamic forces driving fluxes of the associated extensive quantities. Establishing the relation between flows of extensive quantities and the intensive variables representing gradients is a problem in statistical mechanics. Flows (Ji) may be coupled. This is expressed by Onsager's equations. In the regime where both the flows are small and the thermodynamic forces vary slowly, there will be a linear relation between them, parametrized by a matrix of coefficients conventionally denoted L: The Onsager relationsIn the regime where both the flows are small and the thermodynamic forces vary slowly, there will be a linear relation between them, parametrized by a matrix of coefficients conventionally denoted L: The second law of thermodynamics requires that the matrix L be positive definite. Statistical mechanics considerations involving microscopic reversibility of dynamics imply that the matrix L is symmetric. This fact is called the Onsager reciprocal relations. Microscopic reversibility of the dynamics implies that the matrix Lij is symmetrical (Onsagers reciprocal relations). Stationary states and the principle of minimal entropy productionSee also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Non-equilibrium_thermodynamics". A list of authors is available in Wikipedia. |





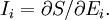
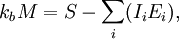
 is Boltzman's constant, whence
is Boltzman's constant, whence