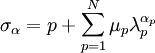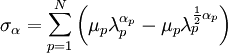To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ogden (hyperelastic model)The Ogden material model is a hyperelastic material model used to describe the non-linear stress-strain behaviour of complex materials such as rubbers and biological tissue. The model relies on the fact that the material behaviour can be described by means of a strain energy density function, whence the stress-strain relationships can be derived. The Ogden model is often used to model rubberlike materials such as polymers, and biological materials. These materials can generally be considered to be isotropic, incompressible and strain rate independent.
Product highlight
Hyperelastic MaterialsFor many materials the standard linear-elastic material models do not accurately describe the observed material behaviour. The most common example of this kind of material is rubber, whose stress-strain relationship can be defined as non-linearly elastic, isotropic, incompressible and generally independent of strain rate. Many biological tissues can also be modelled as these so-called hyperelastic materials.
Strain-Energy PotentialIn continuum mechanics it is postulated that the stress-strain relation of an elastic material follows from a strain-energy potential, which should represent the physical properties of the material under consideration. Consequently there exists a huge number of strain-energy functions and corresponding constitutive theories. The strain energy density function W of an isotropic hyperelastic material can be expressed in terms of the invariants of the Cauchy-Green strain tensor (
with
The strain-energy function of an isotropic material can equivalently be expressed as a function of the eigenvalues of the right Cauchy-Green stretch tensor (
where use is made of the fact that the eigenvalues of tensor
Stress-strain relationshipAfter establishing a suitable strain energy density function W, the 1st Piola-Kirchoff stress tensor can be calculated as
To ensure incompressibility of an elastic material, the strain-energy function can be written in the following form:
where the hydrostatic pressure p functions as a Lagrangian multiplier to enforce the incompressibility constraint. The 1st Piola-Kirchoff stress now becomes
This stress tensor can subsequently be converted into any of the other conventional stress tensors, such as the Cauchy Stress tensor.
Material ModelsLinear Elastic ModelThe simplest model describing the constitutive equations for linear-elastic behaviour is Hooke's law, relating the linearized strain
where the tensor
where λ and μ are the Lamé constants. The stress-strain relationship can then be written as
Hyperelastic ModelsFor rubbery and biological materials, more sophisticated models are necessary. Such materials may exhibit a non-linear stress-strain behaviour at modest strains, or are elastic up to huge strains. These complex non-linear stress-strain behaviours need to be accommodated by specifically tailored strain-energy density functions. The simplest of these hyperelastic models, is the Neo-Hookean solid.
where μ is the shear modulus, which can be determined by experiments. From experiments it is known that for rubbery materials under moderate straining up to 30-70%, the Neo-Hookean model usually fits the material behaviour with sufficient accuracy. To model rubber at high strains, the one-parametric Neo-Hookean model is replaced by more general models, such as the Mooney-Rivlin solid where the strain energy W is a linear combination of two invariants
The Mooney-Rivlin material was originally also developed for rubber, but is today often applied to model (incompressible) biological tissue. For modeling rubbery and biological materials at even higher strains, the more sophisticated Ogden material model has been developed.
Ogden Material ModelIn the Ogden material model, the strain energy density is now expressed in terms of the principal stretches
where N,
In general the shear modulus results from
With N = 3 and by fitting the material parameters, the material behaviour of rubbers can be described very accurately. For particular values of material constants, the Ogden model will reduce to either the Neo-Hookean solid (N = 1, α = 2) or the Mooney-Rivlin material (N = 2, α1 = 2, α2 = − 2). Using the Ogden material model, the three principal values of the Cauchy stresses can now be computed as
where use is made of Uniaxial tensionWe now consider an incompressible material under uniaxial tension, with the stretch ratio given as
The pressure p is determined from incompressibility and boundary condition σ2 = σ3 = 0, yielding:
Relation to other modelsThere exist many models to describe hyperelastic behaviour, each starting from a given strain-energy density function. In practice, however, the Ogden material model has become the reference material law for describing the behaviour of natural rubbers as it combines accuracy with computational simplicity.
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ogden_(hyperelastic_model)". A list of authors is available in Wikipedia. |





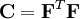 ),
),
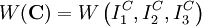
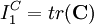
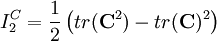
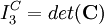
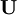 ),
),
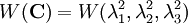
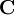 ,
, 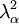 , are the squares of the eigenvalues of tensor
, are the squares of the eigenvalues of tensor 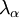 ,
, 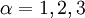 . The eigenvalues
. The eigenvalues 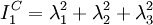
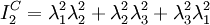
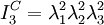
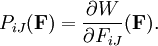
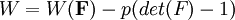
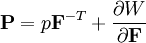 .
.
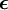 and corresponding stresses
and corresponding stresses 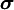 ,
,
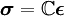
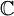 is a function of Young's modulus
is a function of Young's modulus 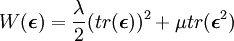
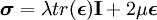
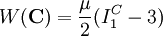
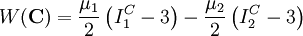
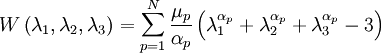
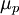 and
and 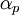 are material constants. Under the assumption of incompressibility one can rewrite as
are material constants. Under the assumption of incompressibility one can rewrite as
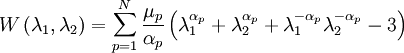
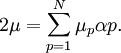
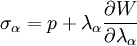
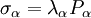 .
.
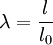 . The principal stresses are given by
. The principal stresses are given by