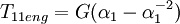To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Neo-Hookean solidNeo-Hookean solid model is an extension of Hooke's law for the case of large deformations. The model of neo-Hookean solid is usable for plastics and rubber-like substances. The response of a neo-Hookean material, or hyperelastic material, to an applied stress differs from that of a linear elastic material. While a linear elastic material has a linear relationship between applied stress and strain, a neo-Hookean material does not. A hyperelastic material will initially be linear, but at a certain point, the stress-strain curve will plateau due to the release of energy as heat while straining the material. Then, at another point, the elastic modulus of the material will increase again. This hyperelasticity, or rubber elasticity, is often observed in polymers. Cross-linked polymers will act in this way because initially the polymer chains can move relative to each other when a stress is applied. However, at a certain point the polymer chains will be stretched to the maximum point that the covalent cross links will allow, and this will cause a dramatic increase in the elastic modulus of the material. One can also use thermodynamics to explain the elasticity of polymers. Product highlight
Neo-Hookean Solid ModelThe model of neo-Hookean solid assumes that the extra stresses due to deformation are proportional to Finger tensor:
where The strain energy for this model is:
where W is potential energy and Usually the model is used for incompressible media. The model was proposed by Ronald Rivlin in 1948. Uni-axial extension
Under uni-axial extension from the definition of Finger tensor: where α1 is the elongation in the stretch ratio in the 1-direction. Assuming no traction on the sides, T22 = T33 = 0, so:
where ε = α1 − 1 is the strain. The equation above is for the true stress (ratio of the elongation force to deformed cross-section), for engineering stress the equation is: For small deformations ε < < 1 we will have:
Thus, the equivalent Young's modulus of a neo-Hookean solid in uniaxial extension is 3G. Simple shearFor the case of simple shear we will have:
where γ is shear deformation. Thus neo-Hookean solid shows linear dependence of shear stresses upon shear deformation and quadratic first difference of normal stresses. GeneralizationThe most important generalisation of Neo-Hookean solid is Mooney-Rivlin solid. Source
Categories: Continuum mechanics | Non-Newtonian fluids | Rubber properties |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Neo-Hookean_solid". A list of authors is available in Wikipedia. |





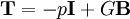 ,
,
 -
-  - is the unity tensor, G is a constant equal to
- is the unity tensor, G is a constant equal to 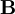 is the
is the 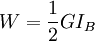 ,
,
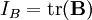 is the trace (or first invariant) of
is the trace (or first invariant) of 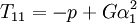
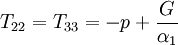
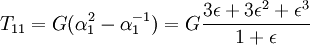 ,
,