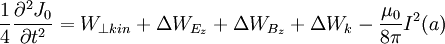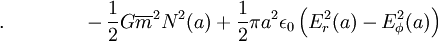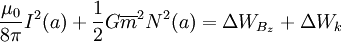To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Pinch (plasma physics)
A pinch is the compression of an electrically conducting filament by magnetic forces. The conductor is usually a plasma, but could also be a solid or liquid metal. In a z-pinch, the current is axial (in the z direction in a cylindrical coordinate system) and the magnetic field azimuthal; in a theta-pinch, the current is azimuthal (in the theta direction in cylindrical coordinates) and the magnetic field is axial. The phenomenon may also be referred to as a "Bennett pinch"[1] (after Willard Harrison Bennett), "electromagnetic pinch"[2], "magnetic pinch"[3], "pinch effect"[4] or "plasma pinch".[5] Pinches occur naturally in electrical discharges such as lightning bolts[6], the aurora[7], current sheets[8], and solar flares[9]. They are also produced in the laboratory, primarily for research into fusion power, but also by hobbyists. Product highlight
Pinch production and typesPinches are created in the laboratory in equipment related to nuclear fusion, such as the Z-pinch machine and high-energy physics, such as the dense plasma focus. Pinches may also become unstable[11], and generate radiation across the electromagnetic spectrum, including radio waves, x-rays[12] and gamma rays[13], and also neutrons[14] and synchrotron radiation[15]. Types of pinches, that may differ in geometry and operating forces[16], include the Cylindrical pinch, Inverse pinch, Orthogonal pinch effect, Reversed field pinch, Sheet pinch, Screw pinch[17] (also called stabalized z-pinch, or θ-z pinch)[18], Theta pinch (or thetatron[19]), Toroidal pinch, Ware pinch [20] and Z-pinch. Pinches are used to generate X-rays, and the intense magnetic fields generated are used in electromagnetic forming of metals (they have been demonstrated in crushing aluminium soft drinks cans[21]). They have applications to particle beams[22] including particle beam weapons[23], and astrophysics[24]. HistoryThe first creation of a z-pinch in the laboratory may have occurred in 1790 in Holland when Martinus van Marum created an explosion by discharging 100 Leyden jars into a wire[26]. The phenomenon was not understood until 1905, when Pollock and Barraclough[10] investigated a compressed and distorted length of copper tube from a lightning rod after it had been struck by lightning. Their analysis showed that the forces due to the interaction of the large current flow with its own magnetic field could have caused the compression and distortion.[27] A similar, and apparently independent, theoretical analysis of the pinch effect in liquid metals was published by Northrupp in 1907.[28]. The next major development was the publication in 1934 of an analysis of the radial pressure balance in a static z-pinch by Bennett[29] (See the following section for details.) Thereafter, the experimental and theoretical progress on pinches was driven by fusion power research. In their article on the "Wire-array z-pinch: a powerful x-ray source for ICF", M G Haines et al, wrote on the "Early history of z-pinches"[30]:
ConfigurationsOne Dimensional configurationsThere are three analytic one dimensional configurations generally studied in plasma physics. These are the θ-pinch, the Z-pinch, and the Screw Pinch. All of the classic one dimensional pinches are cylindrically shaped. Symmetry is assumed in the axial (z) direction and in the azimuthal (θ) direction. It is traditional to name a one-dimensional pinch after the direction in which the current travels. The θ-pinch
The θ-pinch has a magnetic field traveling in the z direction. Using Ampère's law (discarding the displacement term)
Since B is only a function of r we can simplify this to
So J points in the θ direction. θ-pinches tend to be resistant to plasma instabilities. This is due in part to the frozen in flux theorem, which is beyond the scope of this article. The Z-Pinch
The Z-Pinch has a magnetic field in the θ direction. Again, by electrostatic Ampere's Law
So J points in the z direction. Since particles in a plasma basically follow magnetic field lines, Z-pinches lead them around in circles. Therefore, they tend to have excellent confinement properties. The Screw Pinch The Screw pinch is an effort to combine the stability aspects of the θ-pinch and the confinement aspects of the Z-pinch. Referring once again to Ampere's Law
But this time, the B field has a θ component and a z component
So this time J has a component in the z direction and a component in the θ direction. Two Dimensional Equilibria
A common problem with one-dimensional equilibria based machines is end losses. As mentioned above, most of the motion of particles in a plasma is directed along the magnetic field. With the θ-pinch and the screw-pinch, this leads particles to the end of the machine very quickly (as the particles are typically moving quite fast). Additionally, the Z-pinch has major stability problems. Though particles can be reflected to some extent with magnetic mirrors, even these allow many particles to pass. The most common method of mitigating this effect is to bend the cylinder around into a torus. Unfortunately this breaks θ symmetry, as paths on the inner portion (inboard side) of the torus are shorter than similar paths on the outer portion (outboard side). Thus, a new theory is needed. This gives rise to the famous Grad-Shafranov equation. The one dimensional equilibria provide the inspiration for some of the toroidal configurations. An example of this is the ZETA device at Culham England (which also operated as a Reversed Field Pinch). The most well recognized of these devices is the toroidal version of the screw pinch, the Tokamak. Numerical solutions to the Grad-Shafranov equation have also yielded some equilibria, most notably that of the Reversed Field Pinch. Three Dimensional EquilibriaThere does not exist a coherent analytical theory for three-dimensional equilibria. The general approach to finding three dimensional equilibria is to solve the vacuum ideal MHD equations. Numerical solutions have yielded designs for stellarators. Some machines take advantage of simplification techniques such as helical symmetry (for example University of Wisconsin's Helically Symmetric eXperiment). Formal treatment
The Bennett RelationConsider a cylindrical column of fully ionized plasma, with an axial electric field, producing an axial current density, j, and associated azimuthal magnetic field, B. As the current flows through its own magnetic field, a pinch is generated with an inward radial force density of j x B. In a steady state with forces balancing:
where ∇p is the magnetic pressure gradient, pe and pi is the electron and ion pressures. Then using Maxwell's equation ∇ x B = μ0 j and the ideal gas law p = N k T, we derive:
where N is the number of electrons per unit length along the axis, Te and Ti are the electron and ion temperatures, I is the total beam current, and k is the Boltzmann constant. The Generalized Bennett RelationThe Generalized Bennett Relation considers a current-carrying magnetic-field-aligned cylindrical plasma pinch undergoing rotation at angular frequency ω. Along the axis of the plasma cylinder flows a current density jz, resulting in a toroidal magnetίc field Βφ. Originally derived by Witalis, [40] the Generalized Bennett Relation results in [41]:
The positive terms in the equation are expansional forces while the negative terms represent beam compressional forces. The Carlqvist RelationThe Carlqvist Relation, published by Per Carlqvist in 1988[42], is a specialization of the Generalized Bennett Relation (above), for the case that the kinetic pressure is much smaller at the border of the pinch than in the inner parts. It takes the form and is applicable to many space plasmas.
The Carlqvist Relation can be illustrated (see right), showing the total current (I) versus the number of particles per unit length (N) in a Bennett pinch. The chart illustrates four physically distinct regions. The plasma temperature is quite cold (Ti = Te = Tn = 20 K), containing mainly hydrogen with a mean particle mass 3×10-27 kg. The thermokinetic energy Wk >> π a2 pk(a). The curves, ΔWBz show different amounts of excess magnetic energy per unit length due to the axial magnetic field Bz. The plasma is assumed to be non-rotational, and the kinetic pressure at the edges is much smaller than inside. Chart regions: (a) In the top-left region, the pinching force dominates. (b) Towards the bottom, outward kinetic pressures balance inwards magnetic pressure, and the total pressure is constant. (c) To the right of the vertical line ΔWBz=0, the magnetic pressures balances the gravitational pressure, and the pinching force is negligible. (d) To the left of the sloping curve ΔWBz=0, the gravitational force is negligible. Note that the chart shows a special case of the Carlqvist relation, and if it is replaced by the more general Bennett relation, then the designated regions of the chart are not valid. Carlqvist further notes that by using the relations above, and a derivative, it is possible to describe the Bennett pinch, the Jean's criterion (for gravitational instability [43], in one and two dimensions), force-free magnetic fields, gravitationally balanced magnetic pressures, and continuous transitions between these states. Crushing cans with the pinch effect
Many high-voltage electronics enthusiasts make their own devices using pulsed power techniques to produce a theta pinch capable of crushing an aluminium soft drink can by pressure of strong magnetic field. (Warning! High-voltage electric shocks may be lethal). An electromagnetic aluminium can crusher consists of four main components (1) A high voltage DC power supply which provides a source of electrical energy (2) A large energy discharge capacitor to accumulate the electrical energy (3) A high voltage switch or spark gap and (4) A robust coil (capable of surviving high magnetic pressure) through which the stored electrical energy can be quickly discharged in order to generate a correspondingly strong pinching magnetic field (see diagram below). In practice, such a device is somewhat more sophisticated than the schematic diagram suggests, including electrical components that control the current in order to maximize the resulting pinch, and to ensure that the device works safely. For more details, see the notes [44]. Sam Barros's can crusher cost about $500, and uses a large SCR and a 900 Volt capacitor bank storing about 3000 Joules of energy. For a very short time, it generates a magnetic field B~5T (250,000 times the strength of the Earth's magnetic field) which has magnetic pressure P ~ 100 atm. Rate of energy conversion (from electric into magnetic and back) in this device is about 22 megawatts. [45] (Warning! High-voltage electric shocks may be lethal. Do not attempt to build such a device without proper training and precautions.). DepictionsA fictionalized pinch-generating device was used in Ocean's Eleven, where it was used to disrupt Las Vegas's power grid just long enough for the characters to begin their heist.[46] Notes
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Pinch_(plasma_physics)". A list of authors is available in Wikipedia. |





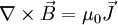
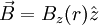
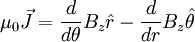
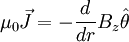
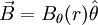
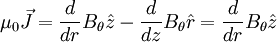
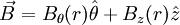
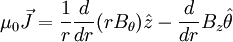
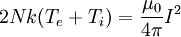 (The Bennett Relation)
(The Bennett Relation)