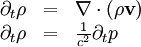To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Pressure-Correction MethodsThis term refers to a class of methods used in computational fluid dynamics for solving the Navier-Stokes equations normally for an incompressible fluid. Product highlight
Common PropertiesThe equations solved in this approach arise from the implicit time integration of the incompressible Navier-Stokes equations. 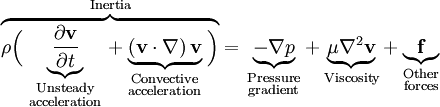 Due to the non-linearity of the convective term in the momentum equation that is written above, this problem is solved with a nested-loop approach. While so called global
or inner iterations represent the real time-steps and are used to update the variables
The correction for the velocity that is obtained from the second equation one has with incompressible flow, the non-divergence criterion or continuity equation 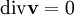 is computed by first calculating a residual value The discretization of this is typically done with either the finite element method or the finite volume method. With the latter, one might also encounter the dual mesh, i.e. the computation grid obtained from connecting the centers of the cells that the initial subdivison into finite elements of the computation domain yielded. Implicit Split-Update ProceduresAnother approach which is typlically used in FEM is the following.
The aim of the correction step is to ensure conservation of mass. In continuous form for compressible substances mass, conservation of mass is expressed by
Applying the divergence operator to the copmpressible momentum equation yields
The idea of pressure-correction also exists in the case of variable density and high Mach numbers, although in this case there is a real physical meaning behind the coupling of dynamic pressure and velocity as arising from the continuity equation References
External links
Categories: Fluid dynamics | Computational fluid dynamics | Equations of fluid dynamics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Pressure-Correction_Methods". A list of authors is available in Wikipedia. |
- Stem-loop
- Potential_energy_surface
- Learn How to Comply with the ISO 8655 Revisions for Pipettes - A Guide to the Routine Testing and Calibration of Pipettes
- EB-Soft Gesellschaft fuer elektronische Beschriftungs-Software mbH - Heilbronn, Germany
- Hunter Associates Laboratory, Inc. - Reston, Stati Uniti d'America





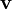 and
and 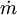 , resulting from spurious mass flux, then using this mass imbalance to get a new pressure value. The pressure value that is attempted to compute, is such that when plugged into momentum equations a divergence-free velocity field results. The mass imbalance is often also used for control of the outer loop.
, resulting from spurious mass flux, then using this mass imbalance to get a new pressure value. The pressure value that is attempted to compute, is such that when plugged into momentum equations a divergence-free velocity field results. The mass imbalance is often also used for control of the outer loop.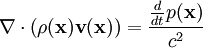
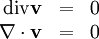 The way of obtaining a velocity field satisfying the above, is to compute a pressure which when substituted into the momentum equation leads to the desired correction of a preliminary computed intermediate velocity.
The way of obtaining a velocity field satisfying the above, is to compute a pressure which when substituted into the momentum equation leads to the desired correction of a preliminary computed intermediate velocity.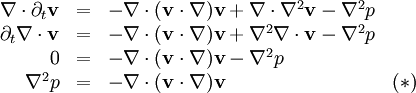
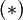 then provides the governing equation for pressure compuation.
then provides the governing equation for pressure compuation.