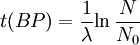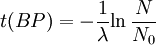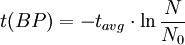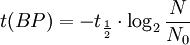To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Radiocarbon datingRadiocarbon dating is a radiometric dating method that uses the naturally occurring isotope carbon-14 (14C) to determine the age of carbonaceous materials up to about 60,000 years.[1] Raw, i.e. uncalibrated, radiocarbon ages are usually reported in radiocarbon years "Before Present" (BP), "Present" being defined as AD 1950. Such raw ages can be calibrated to give calendar dates. The technique of radiocarbon dating was discovered by Willard Libby and his colleagues in 1949[2] during his tenure as a professor at the University of Chicago. Libby estimated that the steady state radioactivity concentration of exchangeable carbon-14 would be about 14 disintegrations per minute (dpm) per gram. In 1960, he was awarded the Nobel Prize in chemistry for this work. One of the frequent uses of the technique is to date organic remains from archaeological sites. Plants fix atmospheric carbon during photosynthesis, so the level of C14 in living plants and animals equals the level of C14 in the atmosphere. Product highlight
Basic physicsCarbon has two stable, nonradioactive isotopes: carbon-12 (12C), and carbon-13 (13C). In addition, there are trace amounts of the unstable isotope carbon-14 (14C) on Earth. Carbon-14 has a half-life of 5730 years and would have long ago vanished from Earth were it not for the unremitting cosmic ray impacts on nitrogen in the Earth's atmosphere, which create more of the isotope. The neutrons resulting from the cosmic ray interactions participate in the following nuclear reaction on the atoms of nitrogen molecules (N2) in the atmospheric air:
The highest rate of carbon-14 production takes place at altitudes of 9 to 15 km (30,000 to 50,000 ft), and at high geomagnetic latitudes, but the carbon-14 spreads evenly throughout the atmosphere and reacts with oxygen to form carbon dioxide. Carbon dioxide also permeates the oceans, dissolving in the water. For approximate analysis it is assumed that the cosmic ray flux is constant over long periods of time; thus carbon-14 is produced at a constant rate and the proportion of radioactive to non-radioactive carbon is constant: ca. 1 part per trillion (600 billion atoms/mole). In 1958 Hessel de Vries showed that the concentration of carbon-14 in the atmosphere varies with time and locality. For the most accurate work, these variations are compensated by means of calibration curves. When these curves are used, their accuracy and shape are the factors that determine the accuracy and age obtained for a given sample. Plants take up atmospheric carbon dioxide by photosynthesis, and are ingested by animals, so every living thing is constantly exchanging carbon-14 with its environment as long as it lives. Once it dies, however, this exchange stops, and the amount of carbon-14 gradually decreases through radioactive beta decay. By emitting an electron and an anti-neutrino, carbon-14 is changed into stable (non-radioactive) nitrogen-14. This decay can be used to measure how long ago once-living material died. However, aquatic plants obtain some of their carbon from dissolved carbonates which are likely to be very old, and thus deficient in the carbon-14 isotope, so the method is less reliable for such materials as well as for samples derived from animals with such plants in their food chain. Computation of ages and datesThe radioactive decay of carbon-14 follows an exponential decay. A quantity is said to be subject to exponential decay if it decreases at a rate proportional to its value. Symbolically, this can be expressed as the following differential equation, where N is the quantity and λ is a positive number called the decay constant: The solution to this equation is:
where, for a given sample of carbonaceous matter:
It can be shown that:
Notice that dates are customarily given in years BP which implies t(BP) = -t because the time arrow for dates runs in reverse direction from the time arrow for the corresponding ages. From these considerations and the above equation, it results: For a raw radiocarbon date: and for a raw radiocarbon age: After replacing values, the raw radiocarbon age becomes any of the following equivalent formulae: using logs base e and the average life: and using logs base 2 and the half-life: Measurements and scalesMeasurements are traditionally made by counting the radioactive decay of individual carbon atoms by gas proportional counting or by liquid scintillation counting, but these are relatively insensitive and subject to relatively large statistical uncertainties for small samples (below about 1g carbon). If there is little carbon-14 to begin with, a half-life that long means that very few of the atoms will decay while their detection is attempted (4 atoms/s) /mol just after death, hence e.g. 1 (atom/s)/mol after 10,000 years). Sensitivity has since been greatly increased by the use of accelerator-based mass-spectrometric (AMS) techniques, where all the 14C atoms can be counted directly, rather than only those decaying during the counting interval allotted for each analysis. The AMS technique allows one to date samples containing only a few milligrams of carbon, although the maximum age reported is still around 60,000 years[3]. Raw radiocarbon ages (i.e., those not calibrated) are usually reported in years "before present" (BP). This is the number of radiocarbon years before 1950, based on a nominal (and assumed constant - see "calibration" below) level of carbon-14 in the atmosphere equal to the 1950 level. They are also based on a slightly-off historic value for the half-life maintained for consistency with older publications (see "Radiocarbon half-life" below). See the section on computation for the basis of the calculations. Corrections for isotopic fractionation have not been included. Radiocarbon labs generally report an uncertainty, e.g., 3000±30BP indicates a standard deviation of 30 radiocarbon years. Traditionally this includes only the statistical counting uncertainty and some labs supply an "error multiplier" that can be multiplied by the uncertainty to account for other sources of error in the measuring process. Additional error is likely to arise from the nature and collection of the sample itself, e.g., a tree may accumulate carbon over a significant period of time. Such old wood, turned into an artifact some time after the death of the tree, will reflect the date of the carbon in the wood. The current maximum radiocarbon age limit lies in the range between 58,000 and 62,000 years (approximately 10 half-lives)(cf refs [1, 3]). This limit is encountered when the radioactivity of the residual 14C in a sample is too low to be distinguished from the background radiation. CalibrationThe need for calibrationA raw BP date cannot be used directly as a calendar date, because the level of atmospheric 14C has not been strictly constant during the span of time that can be radiocarbon dated. The level is affected by variations in the cosmic ray intensity which is affected by variations in the earth's magnetosphere caused by solar storms. In addition there are substantial reservoirs of carbon in organic matter, the ocean, ocean sediments (see methane hydrate), and sedimentary rocks. Changing climate can sometimes disrupt the carbon flow between these reservoirs and the atmosphere. The level has also been affected by human activities—it was almost doubled for a short period due to atomic bomb tests in the 1950s and 1960s and has been reduced by the release of large amounts of CO2 from ancient organic sources where 14C is not present—the fossil fuels used in industry and transportation, known as the Suess effect. The atmospheric 14C concentration may differ substantially from the concentration in local water reservoirs. Eroded from CaCO3 or organic deposits, old carbon may be easily assimilated and provide diluted 14C carbon into trophic chains. Calibration methodsThe raw radiocarbon dates, in BP years, are therefore calibrated to give calendar dates. Standard calibration curves are available, based on comparison of radiocarbon dates of samples that can be independently dated by other methods such as examination of tree growth rings (dendrochronology), ice cores, deep ocean sediment cores, lake sediment varves, coral samples, and speleothems (cave deposits). The calibration curves can vary significantly from a straight line, so comparison of uncalibrated radiocarbon dates (e.g., plotting them on a graph or subtracting dates to give elapsed time) is likely to give misleading results. There are also significant plateaus in the curves, such as the one from 11,000 to 10,000 radiocarbon years BP, which is believed to be associated with changing ocean circulation during the Younger Dryas period. The accuracy of radiocarbon dating is lower for samples originating from such plateau periods. The 2004 version of the calibration curve extends back quite accurately to 26,000 years BP. Any errors in the calibration curve do not contribute more than ±16 years to the measurement error during the historic and late prehistoric periods (0 - 6,000 yrs BP) and no more than ±163 years over the entire 26,000 years of the curve, although its shape can reduce the accuracy as mentioned above.[5] Radiocarbon half-lifeLibby vs Cambridge valuesCarbon dating was developed by a team led by Willard Libby. Originally a carbon-14 half-life of 5568±30 years was used, which is now known as the Libby half-life. Later a more accurate figure of 5730±40 years was determined, which is known as the Cambridge half-life. However, laboratories continue to use the Libby figure to avoid inconsistencies when comparing raw dates and when using calibration curves to obtain calendrical dates. Carbon exchange reservoirLibby's original exchange reservoir hypothesis has recently been criticized by Anatoly Fomenko because of its central assumptions that: (a) the exchange reservoir is constant all over the world; (b) the variations in 14C level are global, such that a small number of samples from a specific year are sufficient for calibration of the dating scale[6]. However, since Libby's early work was published (1950 to 1958), temporal, latitudinal and continental variations in the carbon exchange reservoir have been observed by Hessel de Vries (1958; as reviewed by Lerman et al., 1959, 1960). Subsequently, calibration curves have been developed that allow the correction of raw radiocarbon dates. The reservoir effects that necessitate this correction include:
These effects were first confirmed when samples of wood from around the world, which all had the same age (based on tree ring analysis), showed deviations from the dendrochronological age. Calibration techniques based on tree-ring samples have contributed to increase the accuracy since 1962, when they were accurate to 700 years at worst[11]. Speleothem studies extend 14C calibrationRelatively recent (2001) evidence has allowed scientists to refine the knowledge of one of the underlying assumptions. A peak in the amount of carbon-14 was discovered by scientists studying speleothems in caves in the Bahamas. Stalagmites are calcium carbonate deposits left behind when seepage water, containing dissolved carbon dioxide, evaporates. Carbon-14 levels were found to be twice as high as modern levels[12]. These discoveries improved the calibration for the radiocarbon technique and extended its usefulness to 45,000 years into the past[13]. Examples
See also
Notes
References
Categories: Radiometric dating | Radioactivity | Carbon |
|||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Radiocarbon_dating". A list of authors is available in Wikipedia. | |||||||||||||||||||||





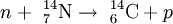
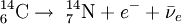
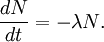
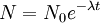 ,
,
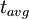 =
=  = radiocarbon mean- or average-life = 8033 years (Libby value)
= radiocarbon mean- or average-life = 8033 years (Libby value)
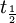 =
= 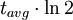 = radiocarbon half-life = 5568 years (Libby value)
= radiocarbon half-life = 5568 years (Libby value)