To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Radius of gyrationRadius of gyration is the name of several related measures of the size of an object, a surface, or an ensemble of points. It is calculated as the root mean square distance of the objects' parts from either its center of gravity or an axis. Product highlight
Applications in structural engineeringIn structural engineering, the two-dimensional radius of gyration is used to describe the distribution of cross sectional area in a beam around its centroidal axis. The radius of gyration is given by the following formula or where I is the second moment of area and A is the total cross-sectional area. The gyration radius is useful in estimating the stiffness of a beam. However, if the principal moments of the two-dimensional gyration tensor are not equal, the beam will tend to buckle around the axis with the smaller principal moment. For example, a beam with an elliptical cross-section will tend to buckle around the axis with the smaller semiaxis. It also can be referred to as the radial distance from a given axis at which the mass of a body could be concentrated without altering the rotational inertia of the body about that axis. In engineering, where people deal with continuous bodies of matter, the radius of gyration is more usually calculated as an integral. Applications in mechanicsThe radius of gyration about a given axis can be computed in terms of the moment of inertia I around that axis, and the total mass M; or It should be noted that I is a scalar, and is not the moment of inertia tensor. [1] Molecular applicationsIn polymer physics, the radius of gyration is used to describe the dimensions of a polymer chain. The radius of gyration of a particular molecule at a given time is defined as: where As a third method, the radius of gyration can also be computed by summing the principal moments of the gyration tensor. Since the chain conformations of a polymer sample are quasi infinite in number and constantly change over time, the "radius of gyration" discussed in polymer physics must usually be understood as a mean over all polymer molecules of the sample and over time. That is, the radius of gyration which is measured is an average over time or ensemble: where the angular brackets An entropically governed polymer chain (i.e. in so called theta conditions) follows a random walk in three dimensions. The radius of gyration for this case is given by Note that, although aN represents the contour length of the polymer, a is strongly dependent of polymer stiffness, and can vary over orders of magnitude. N is reduced accordingly. One reason that the radius of gyration is an interesting property is that it can be determined experimentally with static light scattering as well as with small angle neutron- and x-ray scattering. This allows theoretical polymer physicists to check their models against reality. The hydrodynamic radius is numerically similar, and can be measured with Size exclusion chromatography. Derivation of identityTo show that the two definitions of Carrying out the summation over the last two terms and using the definition of Similarly, we may multiply out the summand of the second definition which can be written: Substituting the definition of
proving the identity of the two definitions. Notes
References
Categories: Solid mechanics | Polymer physics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Radius_of_gyration". A list of authors is available in Wikipedia. |





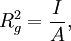
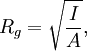
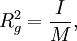
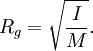
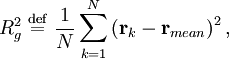
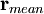 is the mean position of the monomers.
As detailed below, the radius of gyration is also proportional to the root mean square distance between the monomers:
is the mean position of the monomers.
As detailed below, the radius of gyration is also proportional to the root mean square distance between the monomers:
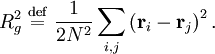
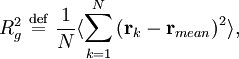
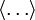 denote the
denote the 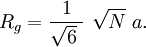
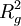 are identical,
we first multiply out the summand in the first definition:
are identical,
we first multiply out the summand in the first definition:
![R_{g}^{2} \ \stackrel{\mathrm{def}}{=}\ \frac{1}{N} \sum_{k=1}^{N} \left( \mathbf{r}_{k} - \mathbf{r}_{mean} \right)^{2} = \frac{1}{N} \sum_{k=1}^{N} \left[ \mathbf{r}_{k} \cdot \mathbf{r}_{k} + \mathbf{r}_{mean} \cdot \mathbf{r}_{mean} - 2 \mathbf{r}_{k} \cdot \mathbf{r}_{mean} \right].](images/math/7/d/1/7d1ad120fadd28a28d829d00757f31fe.png)
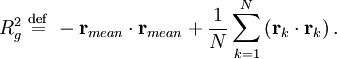
![R_{g}^{2} \ \stackrel{\mathrm{def}}{=}\ \frac{1}{2N^{2}} \sum_{i,j} \left( \mathbf{r}_{i} - \mathbf{r}_{j} \right)^{2} = \frac{1}{2N^{2}} \sum_{i,j} \left[ \mathbf{r}_{i} \cdot \mathbf{r}_{i} + \mathbf{r}_{j} \cdot \mathbf{r}_{j} - 2\mathbf{r}_{i} \cdot \mathbf{r}_{j} \right],](images/math/1/c/e/1ceb4c1bb31b1f52a43412406fb08cb4.png)
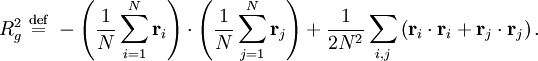
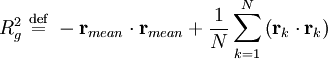 ,
,


