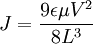To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Space chargeSpace charge is a concept in which excess electric charge is treated as being a continuum of charge distributed over a region of space (either a volume or an area) rather than distinct point-like charges. This model typically applies when charge carriers have been emitted from some region of a solid—the cloud of emitted carriers can form a space charge region if they are sufficiently spread out or the charged atoms, or molecules left behind in the solid can form a space charge region. Space charge usually only occurs in dielectric media (including vacuum) because in a conductive medium the charge tends to be rapidly neutralized or screened. The sign of the space charge can be either negative or positive. This situation is perhaps most familiar in the area near a metal object when it is heated to incandescence in a vacuum. This effect was first observed by Thomas Edison in light bulb filaments, where it is sometimes called the Edison Effect, but space charge is a significant phenomenon in many vacuum and solid-state electronic devices. Product highlight
CausePhysical explanationWhen a metal object is placed in a vacuum and is heated to incandescence, the energy is sufficient to cause electrons to "boil" away from the surface atoms and surround the metal object in a cloud of free electrons. This is called thermionic emission. The resulting cloud is negatively charged, and can be attracted to any nearby positively charged object, thus producing an electrical current which passes through the vacuum. Mathematical explanationIf the "vacuum" has a pressure of 10-6mm or less, the main vehicle of conduction is electrons. The current per cm2 of cathode as a function of cathode temperature is given by:
The emitted electrons do not all have the same but have a Maxwellian distribution of speeds, viz., proportional to where v is the speed, and A0 = The reflection coefficient can be as low as 0.105 but is usually near 0.5. For Tungsten, (1 - ř)A0 = 60 to 100 and φ = 4.52. At 2500°C, the emission is 300mA/cm2. The emission current is many times greater than that normally collected by the electrodes, except in some pulsed valves such as the cavity magnetron used in radar; the cathode would suffer rapid exhaustion if the full emission were drawn off. Most of the electrons emitted by the cathode are driven back to it by the repulsion of the cloud of electrons in its neighborhood. This is called the space charge effect, and it determines the current-voltage characteristic of the tube. OccurrenceSpace charge is an inherent property of all vacuum tubes. This has at times made life harder or easier for electrical engineers who used tubes in their designs. For example, space charge significantly limited the practical application of triode amplifiers because the addition of the grid electrode impedes the flow of electrons from cathode to anode depending on fluctuations in grid voltage. These voltages were thus able to control the amount of space charge able to flow within the envelope. While this allowed for more precise control over current flow, it reduced the gain that could be achieved by such tubes. On the other hand, space charge was useful in some tube applications because it generates a negative EMF within the tube's envelope, which could be used to create a negative bias on the tube's grid. Grid bias could also be achieved by using an applied grid voltage in addition to the control voltage. This could improve the engineer's control and fidelity of amplification. Space charges can also occur within dielectrics. For example, when gas near a high voltage electrode begins to undergo dielectric breakdown, electrical charges are injected into the region near the electrode, forming space charge regions in the surrounding gas. Space charges can also occur within solid or liquid dielectrics that are stressed by high electric fields. Trapped space charges within solid dielectrics are often a contributing factor leading to dielectric failure within high voltage power cables and capacitors. Child's LawAlso known as the Child-Langmuir Law or the Three-Halves Power Law, Child's Law states that the space charge-limited current (SCLC) in a plane-parallel diode varies directly as the three-halves power of the anode voltage Va and inversely as the square of the distance d separating the cathode and the anode. That is,
Where Ia is the anode current, J the current density, and S the area. This assumes the following:
Mott's steady-state space-charge-limited conduction modelThe steady-state space-charge-limited conduction-current density J in a plane-parallel dielectric sample with electrode separation L is proportional to the square of the applied voltage V. That is, This assumes the following:
Shot noiseSpace charge tends to reduce shot noise. Electrons (and positive charge carriers) come with their own built-in negative feedback. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Space_charge". A list of authors is available in Wikipedia. |





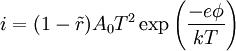 A/cm2
A/cm2
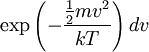
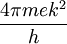 = 120 A/cm2K2
= 120 A/cm2K2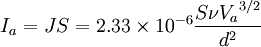 .
.