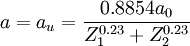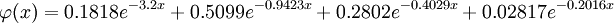To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stopping power (particle radiation)In passing through matter, fast charged particles ionize the atoms or molecules which they encounter. Thus, the fast particles gradually lose energy in many small steps. By stopping power we mean the average energy loss of the particle per unit path length, measured for example in MeV/cm (see figure to the right). Stopping power is a necessary ingredient for many parts of basic science, for medical and for technological applications (ICRU 2005). Product highlight
Stopping power, Bragg curve and rangeThe stopping power depends on the type and energy of the particle and on the properties of the material it passes. Since the production of an ion pair (usually a positive ion and a (negative) electron) requires a fixed amount of energy (for example, 33 eV in air), the density of ionisation along the path is proportional to the stopping power of the material. Both electrons and positive ions lose energy while passing through matter. In the following, we mainly treat positive ions. By 'stopping power', we mean a property of the material, while 'energy loss per unit path length' describes what happens to the particle. But numerical value and units are identical for both quantities; they are usually written with a minus sign in front: where E means energy, and x is the path length. The minus sign makes S positive. The stopping power and hence, the density of ionization, usually increases toward the end of range and reaches a maximum, the Bragg peak, shortly before the energy drops to zero. The curve that describes this is called the Bragg curve. This is of great practical importance for radiation therapy. The picture shows how the stopping power of 5.49 MeV alpha particles increases while the particle traverses air, until it reaches the maximum. This particular energy corresponds to that of the naturally radioactive gas radon (222Rn) which is present in the air in minute amounts wherever the ground contains granite. The mean range can be calculated by integrating the reciprocal stopping power over energy. Electronic and nuclear stoppingBy electronic stopping, one means slowing down due to the inelastic collisions between bound electrons in the medium and the ion moving through it. The term inelastic is used to signify that the collisions may result both in excitations of bound electrons of the medium, and in excitations of the electron cloud of the ion. Since the number of collisions an ion experiences with electrons is large, and since the charge state of the ion while traversing the medium may change frequently, it is very difficult to describe all possible interactions for all possible ion charge states. Instead, the electronic stopping power is often given as a simple function of energy Se(E) which is an average taken over all energy loss processes for different charge states. It can be theoretically determined to an accuracy of a few % in the energy range above several hundred keV per nucleon from theoretical treatments, the best known being the Bethe formula. At energies lower than about 100 keV per nucleon, it becomes more difficult to determine the electronic stopping theoretically (see Sigmund 2005). Graphical presentations of experimental values of the electronic stopping power for many ions in many substances have been given by Paul, see http://www.exphys.uni-linz.ac.at/Stopping/. The accuracy of various stopping tables has been determined, e.g., by (Paul 2006), using statistical comparisons.
By nuclear stopping, one means elastic collisions between the ion and atoms in the sample. If one knows the form of the repulsive potential V(r) between two atoms (see below), it is possible to calculate the nuclear stopping power Sn(E). In the stopping power figure shown above for protons in aluminum, nuclear stopping is negligible except at the lowest energy. Nuclear stopping increases when the mass of the ion increases. In the figure shown here, nuclear stopping is larger than electronis stopping at low energy. For very light ions slowing down in heavy materials, the nuclear stopping is weaker than the electronic at all energies. At not too high energies, the stopping power is therefore the sum of two terms: S(E) = Se(E) + Sn(E). Several semi-empirical stopping power formulas have been devised. The model given by Ziegler, Biersack and Littmark (the so called "ZBL" stopping) (Ziegler 1985), implemented in different versions of the TRIM/SRIM codes (http://www.SRIM.org), is used most often today. Close to the surface, both nuclear and electronic stopping may lead to sputtering. Energy regimesAt very high energies (larger than several hundreds of MeV per nucleon), nuclear reactions and (especially for electrons) bremsstrahlung and Cherenkov radiation contribute to the slowing down of all charged particles (Burcham 1979). The remainder of this article mainly deals with lower energies. The slowing-down process in solidsIn the beginning of the slowing-down process at high energies, the ion is slowed down mainly by electronic stopping, and it moves almost in a straight path. When the ion has slowed down sufficiently, the collisions with nuclei (the nuclear stopping) become more and more probable, finally dominating the slowing down. When atoms of the solid receive significant recoil energies when struck by the ion, they will be removed from their lattice positions, and produce a cascade of further collisions in the material. These collision cascades are the main cause of damage production during ion implantation in metals and semiconductors. The inset in the figure shows a typical range distribution of ions deposited in the solid. The case shown here might for instance be the slowing down of a 1 MeV silicon ion in silicon. The mean range for a 1 MeV ion is typically in the micrometer range. Repulsive interatomic potentialsAt very small distances between the nuclei the repulsive interaction can be regarded as essentially Coulombic. At greater distances, the electron clouds screen the nuclei from each other. Thus the repulsive potential can be described by multiplying the Coulombic repulsion between nuclei with a screening function where A large number of different repulsive potentials and screening functions have been proposed over the years, some determined semi-empirically, others from theoretical calculations. A much used repulsive potential is the one given by Ziegler, Biersack and Littmark, the so called ZBL repulsive potential. It has been constructed by fitting a universal screening function to theoretically obtained potentials calculated for a large variety of atom pairs (Ziegler 1985). The ZBL screening parameter and function have the forms and where x = r / au and a0 is the Bohr atomic radius = 0.529 Å. The standard deviation of the fit of the universal ZBL repulsive potential to the theoretically calculated pair-specific potentials it is fit to is 18 % above 2 eV (Ziegler 1985). Even more accurate repulsive potentials can be obtained from self-consistent total energy calculations using density-functional theory and the local-density approximation (LDA) for electronic exchange and correlation (Nordlund 1996). ChannelingIn crystalline materials the ion may in some instances get "channeled", i.e. get focused into a channel between crystal planes where it experiences almost no collisions with nuclei. Also, the electronic stopping power may be weaker in the channel. Thus the nuclear and electronic stopping do not only depend on material type and density but also on its microscopic structure and cross section. Computer simulations of ion slowing downComputer simulation methods to calculate the motion of ions in a medium have been developed since the 1960s, and are now the dominant way of treating stopping power theoretically. The basic idea in them is to follow the movement of the ion in the medium by simulating the collisions with nuclei in the medium. The electronic stopping power is usually taken into account as a frictional force slowing down the ion. Conventional methods used to calculate ion ranges are based on the binary collision approximation (BCA) (Robinson 1974). In these methods the movement of ions in the implanted sample is treated as a succession of individual collisions between the recoil ion and atoms in the sample. For each individual collision the classical scattering integral is solved by numerical integration. The impact parameter p in the scattering integral is determined either from a stochastic distribution or in a way that takes into account the crystal structure of the sample. The former method is suitable only in simulations of implantation into amorphous materials, as it does not account for channeling. The best known BCA simulation program is TRIM/SRIM (short of TRansport of Ions in Matter, in more recent versions called Stopping and Range of Ions in Matter), which is based on the ZBL electronic stopping and interatomic potential (Biersack 1980, Ziegler 1985, www.SRIM.org). It has a very easy-to-use user interface, and has default parameters for all ions in all materials up to an ion energy of 1 GeV, which has made it immensely popular. However, it doesn't take account of the crystal structure, which severely limits it's usefulness in many cases. Several BCA programs overcome this difficulty; some fairly well-known are MARLOWE (Robinson 1992), BCCRYS and crystal-TRIM. Although the BCA methods have been successfully used in describing many physical processes, they have some obstacles for describing the slowing down process of energetic ions realistically. Due to the basic assumption that collisions are binary, severe problems arise when trying to take multiple interactions into account. Also, in simulating crystalline materials the selection process of the next colliding lattice atom and the impact parameter p always involve several parameters which may not have perfectly well-defined values, which may affect the results 10-20 % even for quite reasonable-seeming choices of the parameter values. The best reliability in BCA is obtained by including multiple collisions in the calculations, which is not easy to do correctly. However, at least MARLOWE does this. A fundamentally more straightforward way to model multiple atomic collisions is provided by molecular dynamics (MD) simulations, in which the time evolution of a system of atoms is calculated by solving the equations of motion numerically. Special MD methods have been devised in which the number of interactions and atoms involved in MD simulations have been reduced in order to make them efficient enough for calculating ion ranges (Nordlund 1995, Beardmore 1998) References and further reading
Categories: Condensed matter physics | Materials science |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stopping_power_(particle_radiation)". A list of authors is available in Wikipedia. |





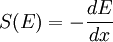
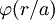 ,
,
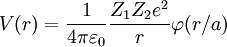
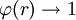 when
when 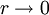 . Here
. Here