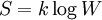Werner Kuhn

Werner Kuhn (1899-1963) is a Swiss physical chemist who developed the first model of the viscosity of polymer solutions using statistical mechanics.^[1] He is known for being the first to apply Boltzmann's entropy formula:^[2]

to the modeling of rubber molecules, i.e. the "rubber band entropy model", molecules which he imagined as chains of N independenly oriented links of length b with an end-to-end distance of r.^[3] This model, which resulted in the derivation of the thermal equation of state of rubber, has since been extrapolated to the entropic modeling of proteins and other conformational polymer chained molecules attached to a surface.

Kuhn received a degree in chemical engineering at the Eidgenössische Technische Hochschule (ETH, Federal Institute of Technology), in Zürich, and later a doctorate (1923) in physical chemistry.^[1]

Additional recommended knowledge

Essential Laboratory Skills Guide

Weighing the right way

Daily Sensitivity Test

Entropy model of rubber

Composition

Aside from a few natural product impurities, natural rubber is essentially a polymer of isoprene units, a hydrocarbon diene monomer. Synthetic rubber can be made as a polymer of isoprene or various other monomers. Rubber is believed to have been named by Joseph Priestley, who discovered in 1770 that dried latex rubbed out pencil marks. The material properties of natural rubber make it an elastomer and a thermoplastic. However it should be noted that as the rubber is vulcanized it will turn into a thermoset. Most rubber in everyday use is vulcanized to a point where it shares properties of both i.e. if it is heated and cooled it is degraded but not destroyed.

Elasticity

In most elastic materials, such as metals used in springs, the elastic behavior is caused by bond distortions. When force is applied, bond lengths deviate from the (minimum energy) equilibrium and strain energy is stored electrostatically. Rubber is often assumed to behave in the same way, but it turns out this is a poor description. Rubber is a curious material because, unlike metals, strain energy is stored thermally, as well as electrostatically.

In its relaxed state rubber consists of long, coiled-up polymer chains that are interlinked at a few points. Between a pair of links each monomer can rotate freely about its neighbour. This gives each section of chain leeway to assume a large number of geometries, like a very loose rope attached to a pair of fixed points. At room temperature rubber stores enough kinetic energy so that each section of chain oscillates chaotically, like the above piece of rope being shaken violently.

When rubber is stretched the "loose pieces of rope" are taut and thus no longer able to oscillate. Their kinetic energy is given off as excess heat. Therefore, the entropy decreases when going from the relaxed to the stretched state, and it increases during relaxation. This change in entropy can also be explained by the fact that a tight section of chain can fold in fewer ways (W) than a loose section of chain, at a given temperature (nb. entropy is defined as S=k*ln(W)). Relaxation of a stretched rubber band is thus driven by an increase in entropy, and the force experienced is not electrostatic, rather it is a result of the thermal energy of the material being converted to kinetic energy. Rubber relaxation is endothermic. The material undergoes adiabatic cooling during contraction. This property of rubber can easily be verified by holding a stretched rubber band to your lips and relaxing it.

Stretching of a rubber band is in some ways equivalent to the compression of an ideal gas, and relaxation in equivalent to its expansion. Note that a compressed gas also exhibits "elastic" properties, for instance inside an inflated car tire. The fact that stretching is equivalent to compression may seem somewhat counter-intuitive, but it makes sense if rubber is viewed as a one-dimensional gas. Stretching reduces the "space" available to each section of chain.

Vulcanization of rubber creates more disulphide bonds between chains so it makes each free section of chain shorter. The result is that the chains tighten more quickly for a given length of strain. This increases the elastic force constant and makes rubber harder and less extendable.

When cooled below the glass transition temperature, the quasi-fluid chain segments "freeze" into fixed geometries and the rubber abruptly loses its elastic properties, though the process is reversible. This is a property it shares with most elastomers. At very cold temperatures rubber is actually rather brittle; it will break into shards when struck or stretched. This critical temperature is the reason that winter tires use a softer version of rubber than normal tires. The failing rubber o-ring seals that contributed to the cause of the Challenger disaster were thought to have cooled below their critical temperature. The disaster happened on an unusually cold day.

References

1. ^ ^{a b} Werner Kuhn - Encyclopedia Britannica
2. ^ Kuhn, W. (1934). "Über die Gestalt fadenförmiger Moleküle in Losungen" (On the shape of filform molecules in solutions). Kolloidzeitschrift 68, p. 2.
3. ^ Müller, Ingo (2007). A History of Thermodynamics - the Doctrine of Energy and Entropy. Springer. ISBN 978-3-540-46226-2.