Density functional theory took a wrong turn recently
The paper explores in detail the intricate relationship between the results of the quantum-chemical calculations and the approximations they rely upon.
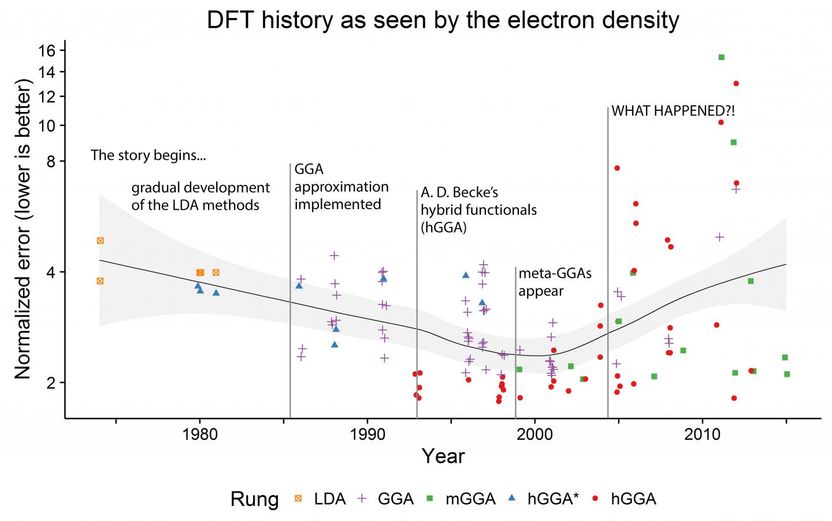
The maximal deviation of the density produced by every DFT method from the exact one (lower is better!). The line shows the average deviation per year, with the light gray area denoting its 95 percent confidence interval.
Ivan S. Bushmarinov
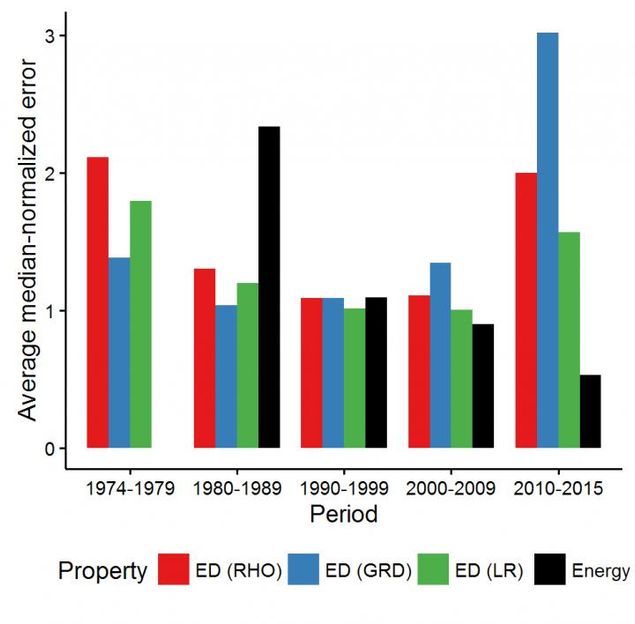
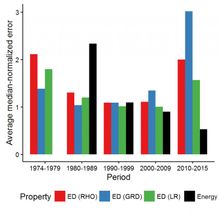
The average density and energy error produced by various DFT methods per decade.
Ivan S. Bushmarinov
When chemists want (or need) to include some "theory" in their papers, it usually means that they will perform some quantum-chemical calculations of the participating molecules. This, strictly speaking, means solving a series of extremely complex equations describing the motion of electrons around atomic nuclei, the target of the calculation being the energies of the starting molecules and the products.
Indeed, a chemist will know almost everything she wants about a reaction if she knows the energies of the participating molecules and the products; and to know the energy of each step leading from one molecule to another is to truly know everything about a process. Similarly, in materials science the energies of the 3D structures serve as a necessary information for prediction of the new materials and the study of their properties.
The exact solution of the underlying Schrödinger's equation for real systems is unreachable in reasonable time; approximations are therefore necessary. However, those obtainable from approximate description of the electron motion either are too simple to reproduce the behavior of many actual molecules (this is the case of the Hartree-Fock method) or again too difficult to compute for large systems (this is the case of the Møller-Plesset perturbation theory and the "heavier" methods).
The breakthrough for computational methods in quantum chemistry came with the density functional theory (DFT) and the Hohenberg-Kohn theorems. The theorems basically say that the average number of electrons located at any one point in space--otherwise called the electron density distribution--contains all the information needed to determine the energy. There is, however, a catch: these theorems do not provide the method for extracting the energy from the electron density. They just say that such a method, the exact functional, exists.
The DFT first appeared in 1927 in the form of Thomas-Fermi model, gained its legitimation in 1964 with the Hohenberg-Kohn proof, and became the method of choice for the material sciences after 1980, when the Generalized Gradient Approximation (GGA) was introduced; and then conquered the isolated molecules simulations after Axel D. Becke implemented hybrid functionals in 1993. Now there are DFT functionals allowing for a very wide range of the computational cost / accuracy ratio. The DFT boosted the chemistry and material science in many ways and basically handed the power of quantum-chemical modeling to users without a strong physical background. In recognition of this fact, Walter Kohn received a half of the 1998 Nobel Prize--the other half went to John A. Pople, who developed many computational methods and was the principal author of an extremely popular computational chemistry program Gaussian.
Dr. Bushmarinov says:
"In our lab, we work a lot with electron density-based approaches to study chemical bonding. My colleague Michael Medvedev, currently a PhD student in our lab, had an idea to test how well different functionals are reproducing the electron density. Not in the vague "let's test it" sense: he decided to check the electron density for the smallest "difficult" systems out there. These systems are atoms and atomic ions with 2, 4 or 10 electrons. We also chucked some anions in initially for good measure. Well, you might ask a question along the lines of "exactly which insight do you expect to gain from modeling F5+? This particle has much more in common with plasma physics than with chemistry!" I asked such questions myself, I must admit."
Mr. Medvedev, calculated the electron densities and their derivatives for the test atomic species using almost every "named" functional available in major modern computational chemistry codes, as well as many combinations of those: more than 100 in total. He noticed that the quality of the electron density (ED) seemed to worsen over the years despite the improvements in energies reported in the literature, which raised major questions about the state of the modern DFT. Dr. Bushmarinov developed a rigorous way to compare the produced electron densities to the exact one and to produce a rating of the functionals sorted by the quality of their densities.
The problem is, the electron density is not just 'some' property of the system. The Honenberg-Kohn theorem does not say that the energy of a system can be extracted from just any electron distribution; it states that the exact energy should arise from the exact density.
Mr. Medvedev says:
"All functionals currently in use are approximations of the exact functional; so how on Earth can they provide better energies from worse densities? On a philosophical level, this seems to contradict the principle known to any programmer: an algorithm should not produce correct results from faulty data."
At this point, I.S.B and M.M.G. contacted Prof. John P. Perdew of Temple University, for an expert opinion and a collaboration.
Prof. Perdew pointed out a fundamental flaw in the tests initially used (it turned out the anions should not have been used after all) and helped with all theoretical aspects of the paper. Dr. Jianwei Sun performed the necessary computations using the latest methods developed by J.P.P. and him.
Dr. Bushmarinov says:
"After the actual systematic errors were weeded out, the data became beautiful. Just from the RMSD of the electron density you can see the whole history of DFT in a plot. Basically, until early 2000s the densities improved along with the theoretical advances. You can even see the functional hierarchy, for which John Perdew in 2001 coined a term "Jacob's ladder": functionals become more complex and describe everything better as you go from LDA to GGA to mGGA to hGGA. Until, well, something happens which makes a large fraction of the modern functionals worse than the 1974 ones."
The actual lists of the worst and the best functionals provided an answer to this apparent conundrum. The "best" functionals all happened to be derived from solid theoretical approaches--using several routes taken by different groups.
The "worst" methods, however, are only of two kinds. Either they are the pre-1985 ones (the theory was not yet ready), or they were fully obtained by the so-called parameterization. Most of those were developed by a taking flexible functional equation and tuning all ca. 20 parameters with the aim of obtaining the best energies and geometries on a given dataset (usually low hundreds of molecules). Such approach provided excellent energies and geometries, in particular on the test sets normally used for functionals' comparison.
The chemical space is, however, vast, and a method performing well on hundreds of molecules can fail when tested on something it was not trained to reproduce--like small, simple atoms in this study. It should be noted that some of these "misbehaving" methods are actually very popular. Since they contradict the basics of the theory--they yield "good" energies from "bad" densities--the authors concluded that these methods most likely suffer from some internal problems. And the density functional theory will stray further from the path toward the exact functional if this approach to functional developments is not put in check.
Original publication
Other news from the department science
Get the chemical industry in your inbox
From now on, don't miss a thing: Our newsletter for the chemical industry, analytics, lab technology and process engineering brings you up to date every Tuesday and Thursday. The latest industry news, product highlights and innovations - compact and easy to understand in your inbox. Researched by us so you don't have to.
