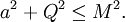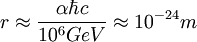Black hole electron

In physics, there is a speculative notion that if there were a black hole with the same mass and charge as an electron, it would share many of the properties of the electron including the magnetic moment and Compton wavelength.

Additional recommended knowledge

Correct Test Weight Handling Guide: 12 Practical Tips

Essential Laboratory Skills Guide

Daily Sensitivity Test

Overview

The discussion of this idea apparently dates as far back as 1919 and was known to Sir Arthur Eddington. More recently, the suggestion has been made by Brian Greene in his book The Elegant Universe. Taken literally, the core idea is that the electron may be a micro black hole, not just resemble it. The idea is appealing for several reasons. To this date, there are no verified theories for the unification of quantum mechanics and gravitation. Furthermore, the Standard Model, although a marvelously successful theory of high-energy physics, has many fundamental particles and adjustable parameters in it. In his book "Geons, Black Holes, and Quantum Foam" John Wheeler writes,"All of physics, both classical and quantum, faces a conceptual problem in dealing with point particles. We think of electrons and neutrons and quarks as existing at mathematical points. We think of photons being created and being absorbed at mathematical points. Yet we cannot really deal with the infinite density of mass or the infinite density of charge implied by point particles and point interactions. These points are annoying pinpricks in the body of physics. We endure them because we have to, while hoping that someday we will identify and understand an inner structure in what today seem to be points". It is known that the electron negative electric charge elements repel one another so that a force is required to hold the electron together. No combination of electric and magnetic forces has been proposed that can produce a stable state. Some theorists, including Brian Greene and Malcolm MacGregor, have indicated that gravitational forces could provide stability. In his book The Elegant Universe Brian Greene wrote; "For many years, some of the most accomplished theoretical physicists speculated about the possibility of space-tearing processes and of a connection between black holes and elementary particles. Although such speculations might have sounded like science fiction at first, the discovery of string theory, with its ability to merge general relativity and quantum mechanics, has allowed us now to plant these possibilities firmly at the forefront of cutting-edge science," (333). Malcolm MacGregor, in his book, The Enigmatic Electron (page 71) noted that gravitational forces could solve the stability problem if the electron is extremely small and dense. Thus, a speculative, basic-principles approach of this type may be useful.

The concept

In general relativity there is no minimum mass for a black hole and there is no gravitational time dilation limit, other than (the unrealistic) zero seconds per second. Very small-mass black holes would look like elementary particles because they would be completely defined by their mass, charge and spin. Their uncertainty of position would be defined by their diameter.

The Kerr-Newman black hole is a solution to the Einstein equations for a black hole with charge and spin. The spin of a Kerr-Newman black hole has no exact counterpart in the classical world. The extreme time dilation required at the photon capture radius indicates that the electron gravitational field has a ring singularity. This ring singularity could be described as a closed-loop vibrating string. Black hole theory predicts that a black hole with charge and spin will have magnetic moment equal to the charge times angular momentum divided by mass, which is equal to the Dirac electron magnetic moment. However, the correct result for the electron magnetic moment contains a small, but very precisely measured, correction from emission and re-absorption of virtual photons.

In 1955, John Archibald Wheeler explored this concept, describing a structure he named a geon. He found that while the structure was interesting, it was unstable. He suggested that geons could provide an intermediate stage in the creation of micro black holes and, since geons are not stable, a geon might radiate away some of its energy in electron-positron pairs. Wheeler also worked on the concept that the things we call particles (electrons) can be accounted for by an inner spacetime structure. A quote from the book Gravitation by Misner, Thorne and Wheeler (page 1215) relates to this concept; "What else can a particle (electron) be but a fossil from the most violent event of all, gravitational collapse?".

A paper titled "Is the electron a photon with toroidal topology?" by J. G. Williamson and M. B. van der Mark, describes an electron model consisting of a photon confined in a closed loop. In this paper, the confinement method is not explained. The Wheeler suggestion of gravitational collapse with conserved angular momentum and charge would explain the required confinement. With confinement explained, this model is consistent with many electron properties. This paper argues (page 20) "--that there exists a confined single-wavelength photon state, (that) leads to a model with non-trivial topology which allows a surprising number of the fundamental properties of the electron to be described within a single framework."

Problems

As a description, the black hole electron theory is incomplete. The first problem is that black holes tend to merge when they meet. Therefore, a collection of black-hole electrons would be expected to become one big black hole. Also, an electron-positron collision would be expected to produce a larger neutral black hole instead of two photons as is observed. These problems reflect the non-quantum nature of general relativity theory.

A more serious issue is Hawking radiation. According to Hawking's theory, a black hole the size and mass of an electron should vanish in a shower of photons (not just two photons of a given energy) within a small fraction of a second. Again, the current incompatibility of general relativity and quantum mechanics at electron scales prevents us from understanding why this never occurs.

The Kerr-Newman metric used to represent a charged, rotating black hole in General Relativity has three specifiable parameters: the mass of the hole, M; the charge of the hole, Q; and the angular momentum per unit mass, a. This metric defines a black hole with an event horizon only when these quantities satisfy the relation

An electron's a and Q (suitably specified in geometrized units) both exceed its mass M. Using these values in the Kerr-Newman solution yields a superextreme Kerr-Newman metric. This metric has no event horizons and thus no black hole, only a naked, spinning ring singularity. A superextreme metric has many seemingly unphysical properties, the most severe being the ring's violation of the cosmic censorship hypothesis and appearance of causality-violating closed timelike curves in the immediate vicinity of the ring.

For these reasons, this speculation is considered a 'toy model', an at best incomplete description of the nature of an electron.

Schwarzschild radius

The Schwarzschild radius (r_s) of any mass is calculated using the following formula:

r_s = 2Gm/c²

For an electron,

G is Newton's gravitational constant,

m is the mass of the electron = 9.109×10⁻³¹kg, and

c is the speed of light.

This gives a value

r_e = 1.353×10⁻⁵⁷m

So if the electron has a radius as small as this, it would become a gravitational singularity. It would then have a number of properties in common with black holes. In accordance with black hole theory, it is required to have maximal angular momentum so that it does not have elevated temperature. The angular momentum value is required to be h bar/2. Without elevated temperature it will not lose mass by Hawking radiation. For a rotating black hole, the Kerr metric equations apply. The intrinsic singularity will then be a ring that lies in the equatorial plane of the particle with a radius value larger than 2Gm/c squared. The radius value 3Gm/c squared is compatible with h bar/2 angular momentum. With this radius (ring) singularity, the electron would be a superextreme black hole with a = 3M rather than an "extreme Kerr" black hole with a = M (using geometrized units). The Russian theorist Alexander Burinskii, in his paper titled, The Dirac-Kerr electron, noted that the electron angular momentum (h bar/2) is so high that black hole horizons disappear and the electron particle is a naked singular ring. Some theorists, including Stephen Hawking and Kip Thorne, have recently concluded that the laws of nature do permit the formation of a naked singularity during gravitational collapse. In a later paper (2007) titled, Kerr Geometry as Space-Time Structure of the Dirac Electron, Burinskii writes:"In this work we obtain an exact correspondence between the wave function of the Dirac equation and the spinor (twistorial) structure of the Kerr geometry. It allows us to assume that the Kerr-Newman geometry reflects the specific space-time structure of electron, and electron contains really the Kerr-Newman circular string of Compton size".

At the radius 3Gm/c squared, a special space curvature condition is found. An electromagnetic wave has a 50 percent probability of either orbiting and spiraling inward or spiraling away to infinity due to the gravitational space curvature at 3Gm/c squared. The radius 3Gm/c squared is the gravitational photon capture radius. This radius is critical if self-gravitational attraction is required to produce a stable state. A photon, confined by its self-gravitational attraction would have toroidal topology, as described in the paper by J.G. Williamson and M.B. van der Mark noted under, The concept.

The ratio, 4 pi times 3Gm/c squared, divided by the electron Compton wavelength is 1.0508x10 exp -44 to one. The square root of this ratio will be the implied gravitational time dilation ratio or photon blueshift ratio at the electron mass photon capture radius. This ratio, 1.0251x10 exp -22 to one, is equal to 4 pi times Planck length times (3/2) exp 1/2, divided by the electron Compton wavelength.

The classical electron radius of 2.818×10⁻¹⁵ meters is substantially larger than its Schwarzschild radius. Standard quantum electrodynamics (QED) theory treats the electron as a point particle, a view completely supported by experiment. Practically, though, particle experiments cannot probe arbitrarily large energy scales, and so QED-based experiments bound the electron radius to a value smaller than the Compton wavelength of a large mass, on the order of 10⁶ GeV, or

See also

• Quantum gravity

References

• Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe. (2004) Jonathan Cape, London.
• S. W. Hawking, Monthly Notices of the Royal Astronomical Society, 152 (1971) 75.
• Abdus Salam, chapter in Quantum Gravity: an Oxford Symposium, Eds. Isham, Penrose and Sciama, Oxford University Press.
• G. 't Hooft, The black hole interpretation of string theory Nuclear Physics B, 335 (1990) 138-154.
• M. J. Duff, Kaluza-Klein Theory in Perspective, (1994).
• A. Burinskii, The Dirac-Kerr electron, (2005) preprint.
• J. G. Williamson & M. B. van der Mark, Is the electron a photon with toroidal topology? Annales de la Fondation Louis de Broglie, Volume 22, no.2, 133 (1997).
• A. Burinskii, Kerr Geometry as Space-Time Structure of the Dirac Electron, (4 Dec 2007).

Popular literature

• Brian Greene, The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory (1999), (See chapter 13)
• John A. Wheeler, Geons, Black Holes & Quantum Foam (1998), (See chapter 10)