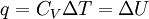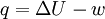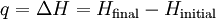To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Calorimetry
Calorimetry is the science of measuring the heat of chemical reactions or physical changes. Calorimetry involves the use of a calorimeter. The word calorimetry is derived from the Latin word calor, meaning heat. Scottish physician and scientist Joseph Black, who was the first to recognize the distinction between heat and temperature, is said to be the founder of calorimetry.[1] Indirect calorimetry calculates heat that living organisms produce from their production of carbon dioxide and nitrogen waste (frequently ammonia in aquatic organisms, or urea in terrestrial ones), OR from their consumption of oxygen. Lavoisier noted in 1780 that heat production can be predicted from oxygen consumption this way, using multiple regression. The Dynamic Energy Budget theory explains why this procedure is correct. Of course, heat generated by living organisms may also be measured by direct calorimetry, in which the entire organism is placed inside the calorimeter for the measurement. Product highlight
Constant-volumeConstant-volume calorimetry is calorimetry performed at a constant volume. This involves the use of a constant-volume calorimeter. No work is performed in constant-volume calorimetry, so the heat measured equals the change in internal energy of the system. The equation for constant-volume calorimetry is (the heat capacity at constant volume is assumed to be constant): where
Since in constant-volume calorimetry the pressure is not kept constant, the heat measured does not represent the enthalpy ch Constant-pressureConstant-pressure calorimetry is calorimetry performed at a constant pressure. This involves the use of a constant-pressure calorimeter. The heat measured equals the change in internal energy of the system minus the work performed: Since in constant-pressure calorimetry, pressure is kept constant, the heat measured represents the enthalpy change: This formula is a simplified representative of Hess's Law. See also
References
Categories: Heat | Thermodynamics | Calorimetry |
|||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Calorimetry". A list of authors is available in Wikipedia. | |||||||||||||