To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Critical phenomenaIn physics, critical phenomena is the collective name associated with the physics of critical points. Most of them stem from the divergence of the correlation length. Critical phenomena include scaling relations among different quantities, power-law divergences of some quantities (such as the magnetic susceptibility in the ferromagnetic phase transition) described by critical exponents, universality, fractal behaviour, ergodicity breaking. Critical phenomena take place in second order phase transition, although not exclusively. The critical behavior is often different from the mean-field approximation which is valid away from the phase transition, since the latter neglects correlations, which become increasingly important as the system approaches the critical point where the correlation length diverges. Many properties of the critical behavior of a system can be derived in the framework of the renormalization group. In order to explain the physical origin of these phenomena, we shall use the Ising model as a pedagogical example. Product highlight
The critical point of the 2D Ising modelLet us consider a 2D square array of classical spins which may only take two positions: +1 and −1, at a certain temperature T, interacting through the Ising classical Hamiltonian: where the sum is extended over the pairs of nearest neighbours and J is a coupling constant, which we will consider to be fixed. There is a certain temperature, called the Curie temperature or critical temperature, Tc below which the system presents ferromagnetic long range order. Above it, it is paramagnetic and is apparently disordered. At temperature zero, the system may only take one global sign, either +1 or -1. At higher temperatures, but below Tc, the state is still globally magnetized, but clusters of the opposite sign appears. As the temperature increases, these clusters start to contain smaller clusters themselves, in a typical Russian dolls picture. Their typical size, called the correlation length, ξ grows with temperature until it diverges at Tc. This means that the whole system is such a cluster, and there is no global magnetization. Above that temperature, the system is globally disordered, but with ordered clusters within it, whose size is again called correlation length, but it is now decreasing with temperature. At infinite temperature, it is again zero, with the system fully disordered. Divergences at the critical pointThe correlation length diverges at the critical point: as The most important is susceptibility. Let us apply a very small magnetic field to the system in the critical point. A very small magnetic field is not able to magnetize a large coherent cluster, but with these fractal clusters the picture changes. It affects easily the smallest size clusters, since they have a nearly paramagnetic behaviour. But this change, in its turn, affects the next-scale clusters, and the perturbation climbs the ladder until the whole system changes radically. Thus, critical systems are very sensitive to small changes in the environment. Other observables, such as the specific heat, may also diverge at this point. All these divergences stem from that of the correlation length. Critical exponents and universalityAs we approach the critical point, these diverging observables behave as Critical dynamicsCritical phenomena may also appear for dynamic quantities, not only for static ones. In fact, the divergence of the characteristic time τ of a system is directly related to the divergence of the thermal correlation length ξ by the introduction of a dynamical exponent z and the relation Ergodicity breakingErgodicity is the assumption that a system, at a given temperature, explores the full phase space, just each state takes different probabilities. In an Ising ferromagnet below Tc this does not happen. If T < Tc, never mind how close they are, the system has chosen a global magnetization, and the phase space is divided into two regions. From one of them it is impossible to reach the other, unless a magnetic field is applied, or temperature is raised above Tc. See also superselection sector Mathematical toolsThe main mathematical tools to study critical points are renormalization group, which takes advantage of the Russian dolls picture to explain universality and predict numerically the critical exponents, and Variational perturbation theory, which converts divergent perturbation expansions into convergent strong-coupling expansions relevant to critical phenomena. In two-dimensional systems, Conformal field theory is a powerful tool which has discovered many new properties of 2D critical systems, employing the fact that scale invariance, along with a few other requisites, leads to an infinite symmetry group. See also
Bibliography
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Critical_phenomena". A list of authors is available in Wikipedia. |





![H= -J \sum_{[i,j]} S_i\cdot S_j](images/math/d/4/8/d486af2363f5033ad9a68cbea4df3722.png)
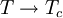 ,
, 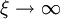 . This divergence poses no physical problem. Other physical observables diverge at this point, leading to some confusion at the beginning.
. This divergence poses no physical problem. Other physical observables diverge at this point, leading to some confusion at the beginning.
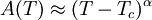 for some exponent
for some exponent 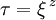 . The voluminous static universality class of a system splits into different, less voluminous dynamic universality classes with different values of z
but a common static critical behaviour.
. The voluminous static universality class of a system splits into different, less voluminous dynamic universality classes with different values of z
but a common static critical behaviour.


