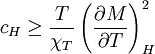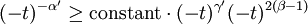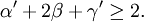To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rushbrooke inequalityIn statistical mechanics, the Rushbrooke inequality relates the critical exponents of a magnetic system which exhibits a first-order phase transition in the thermodynamic limit for non-zero temperature T. Product highlightSince the Helmholtz free energy is extensive, the normalization to free energy per site is given as The magnetization M per site in the thermodynamic limit, depending on the external magnetic field H and temperature T is given by where σi is the spin at the i-th site, and the magnetic susceptibility and specific heat at constant temperature and field are given by, respectively and DefinitionsThe critical exponents α,α',β,γ,γ' and δ are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
where measures the temperature relative to the critical point. DerivationFor the magnetic analogue of the Maxwell relations for the response functions, the relation follows, and with thermodynamic stability requiring that which, under the conditions H = 0,t < 0 and the definition of the critical exponents gives which gives the Rushbrooke inequality Remarkably, in experiment and in exactly solved models, the inequality actually holds as an equality. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rushbrooke_inequality". A list of authors is available in Wikipedia. |





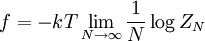
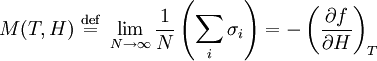
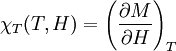
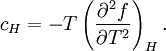
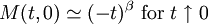
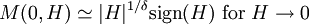
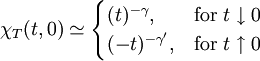
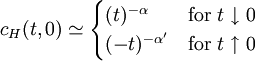
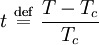
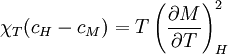
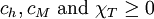 , one has
, one has