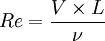To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Foil (fluid mechanics)A foil is a surface designed to maximize lift (force generated perpendicular to the fluid flow) while minimizing drag (force generated in the direction of the fluid flow) in a given range of conditions. Foils may be designed to operate in any fluid, such as air or water. Product highlightPhysics of foilsFoil design is strongly influenced by Bernoulli's principle, which states that high speed fluid flow results in lower pressure on surfaces parallel to the flow, and the related Coanda Effect, which states that a fluid stream will follow a surface that curves away. The traditional curved upper surface and nearly flat lower surface of a wing are designed to accelerate airflow over the curved top surface, and deflect it downwards at the rear. This downwards deflection of air is balanced (according to Newton's Third Law) by a matching upwards force on the foil, which is the lift. It is a common misconception that the pressure differential (caused by the Bernoulli principle) is the direct cause of lift, but the Bernoulli principle is only the means for generating the deflection. Examination of foils in operation shows a significant deflection of the fluid flow downstream of the foil. The three mechanisms all work closely together to generate the greatest amount of lift. The faster the fluid flows over the foil's surface, the more suction is generated, resulting in a stronger Coanda Effect, which results in a greater deflection and more lift. When the forces are right to keep the fluid flow attached to the surface of the foil, it is called laminar flow. If there is insufficient suction to keep the fluid flow attached to the foil's surface, then the flow will separate and become turbulent. This turbulent flow often results in less deflection, loss of lift, and increased drag. Basic design considerationsThe degenerate case of a foil is a simple flat plate. When set at an angle (the angle of attack) to the flow of the fluid it works in, the plate will deflect the fluid passing over and under it, and this deflection will result in a reacting force that pushes, or lifts the plate. In a perfect fluid, that has inertia but no viscosity, a flat plate would be a perfect airfoil, because it would generate lift with no drag. However, once viscosity is added to the equation, drag appears, and the flat plate is no longer an ideal solution--while it does generate lift, it also generates a large amount of drag. Since even a simple flat plate can generate lift, the primary purpose of a foil designed for a given purpose is not the generation of lift, but rather the minimizing of drag under certain conditions. A good example of this is the rudder of a boat or aircraft. Under normal, non-steering conditions, the rudder is not producing any lift--if it were, the craft would turn in response to the lifting force. A primary goal when designing a rudder, therefore, is the minimization the amount of drag it produces when in its neutral state, which is balanced with the need to produce sufficient lift with increasing angle of attack to turn the craft at a reasonable rate at the speeds at which it will be operating. A good example of foils of this type are symmetric NACA 00xx foils, which have very low drag at zero angles of attack, and will generate lift equally well with positive or negative angles of attack.
The formula for a NACA 00xx foil, with "xx" being replaced by the percentage of thickness to chord, is:
where:
The leading edge approximates a cylinder with a radius of:
Since wings generally are used primarily to generate lift in one direction, they are most often asymmetric, generating a better lift to drag ratio with positive angles of attack than with negative angles of attack (although they will work upside down, as stunt pilots often demonstrate when flying upside down). Asymmetric foils will generate some lift at a zero angle of attack.
The simplest asymmetric foils are the NACA 4 digit series foils, which use the same formula as that used to generate the 00xx symmetric foils, but with the line of mean camber bent. The formula used to calculate the mean camber line is:
where:
Reynolds numbersReynolds numbers are used to predict changes in scale or viscosity on a given foil shape.
where:
The kinematic viscosity for water is approximately 1×10-6 m2/s and for air is approximately 15×10-6 m2/s. An easy numeric example in SI units for an airfoil at the transition between laminar and turbulent flow (Re = 106) (could be a sailplane):
Sometimes the transition is shifted to higher Re by means of a clean and smooth surface and sometimes it is shifted to lower Re by means of Vortex generators. The latter is unique to wings. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Foil_(fluid_mechanics)". A list of authors is available in Wikipedia. |





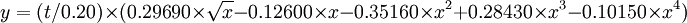
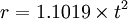
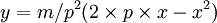 from x = 0 to x = p
from x = 0 to x = p
![y = m / (1 - p)^2 [(1 - 2 \times p) + 2 \times p \times x - x^2]](images/math/5/f/8/5f8b0edae4a1f53a3e0933c2d2879e7b.png) from x = p to x = c
from x = p to x = c