To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hasegawa-Mima equationThe Hasegawa-Mima equation, named after Akira Hasegawa and Kunioki Mima, is an equation that describes a certain regime of plasma, where the time scales are very fast, and the distance scale in the direction of the magnetic field is long. In particular the equation is useful for describing turbulence in some tokamaks. The equation was introduced in Hasegawa and Mima's paper submitted in 1977 to Physics of Fluids, where they compared it to the results of the ATC tokamak. Product highlight
Assumptions
The equationThe Hasegawa-Mima equation is a second order nonlinear partial differential equation that describes the electric potential. The form of the equation is: Although the quasi neutrality condition holds, the small differences in density between the electrons and the ions cause an electric potential. The Hasegawa-Mima equation is derived from the continuity equation: The fluid velocity can be approximated by the E cross B drift: Previous models derived their equations from this approximation. The divergence of the E cross B drift is zero, which keeps the fluid incompressible. However, the compressibility of the fluid is very important in describing the evolution of the system. Hasegawa and Mima argued that the assumption was invalid. The Hasegawa-Mima equation introduces a second order term for the fluid velocity known as the polarization drift in order to find the divergence of the fluid velocity. Due to the assumption of large magnetic field, the polarization drift is much smaller than the E cross B drift. Nevertheless, it introduces important physics. For a two-dimensional incompressible fluid which is not a plasma, the Navier-Stokes equations say: after taking the curl of the momentum balance equation. This equation is almost identical to the Hasegawa-Mima equation except the second and fourth terms are gone, and the electric potential is replaced with the fluid velocity vector potential where: The first and third terms to the Hasegawa-Mima equation, which are the same as the Navier Stokes equation, are the terms introduced by adding the polarization drift. In the limit where the wavelength of a perturbation of the electric potential is much smaller than the gyroradius based on the sound speed, the Hasegawa-Mima equations become the same as the two-dimensional incompressible fluid. NormalizationOne way to understand an equation more fully is to understand what it is normalized to, which gives you an idea of the scales of interest. The time, position, and electric potential are normalized to t',x', and φ' The time scale for the Hasegawa-Mima equation is the inverse ion gyrofrequency: From the large magnetic field assumption the normalized time is very small. However, it is still large enough to get information out of it. The distance scale is the gyroradius based on the sound speed: If you transform to k-space, it is clear that when k, the wavenumber, is much larger than one, the terms that make the Hasegawa-Mima equation differ from the equation derived from Navier-Stokes equation in a two dimensional incompressible flow become much smaller than the rest. From the distance and time scales we can determine the scale for velocities. This turns out to be the sound speed. The Hasegawa-Mima equation, shows us the dynamics of fast moving sounds as opposed to the slower dynamics such as flows that are captured in the MHD equations. The motion is even faster than the sound speed given that the time scales are much smaller than the time normalization. The potential is normalized to: Since the electrons fit a Maxwellian and the quasineutrality condition holds, this normalized potential is small, but similar order to the normalized time derivative. The entire equation without normalization is: Although the time derivative divided by the cyclotron frequency is much smaller than unity, and the normalized electric potential is much smaller than unity, as long as the gradient is on the order of one, both terms are comparable to the nonlinear term. The unperturbed density gradient can also be just as small as the normalized electric potential and be comparable to the other terms. Other forms of the equationOften the Hasegawa-Mima equation is expressed in a different form using Poisson brackets. These Poisson brackets are defined as: Using these Poisson brackets, the equation can be reexpressed as: Often the particle density is assumed to vary uniformly just in one direction, and the equation is written in a sightly different form. The Poisson bracket including the density is replaced with the definition of the Poisson bracket, and a constant replaces the derivative of the density dependent term. Conserved quantitiesThere are two quantities that are conserved in a two-dimensional incompressible fluid. The kinetic energy: And the enstrophy: For the Hasegawa-Mima equation, there are also two conserved quantities, that are related to the above quantities. The generalized energy: And the generalized enstrophy: In the limit where the Hasegawa-Mima equation is the same as an incompressible fluid, the generalized energy, and enstrophy become the same as the kinetic energy and enstrophy. See AlsoHasegawa, A., and Mima, K., Stationary spectrum of strong turbulence in magnetized nonuniform plasma, Phys. Rev. Lett. 39 205 (1977). Categories: Plasma physics | Equations of fluid dynamics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hasegawa-Mima_equation". A list of authors is available in Wikipedia. |





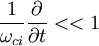
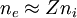
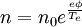
![\frac{\partial}{\partial t}\left(\nabla^2\phi-\phi\right)-\left[\left(\nabla\phi\times \mathbf{\hat z}\right)\cdot\nabla\right]\left[\nabla^2\phi-ln\left(\frac{n_0}{\omega_{ci}}\right)\right]=0](images/math/3/3/6/336b7ee98c9414e00d58788505cf3c01.png)
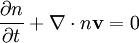
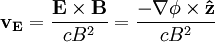
![\frac{\partial}{\partial t}\left(\nabla^2\psi\right)-\left[\left(\nabla\psi\times \mathbf{\hat z}\right)\cdot\nabla\right]\nabla^2\psi =0](images/math/5/8/b/58b89e842a7fb33b4956b04215cbb0f2.png)
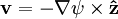


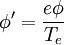
![\frac{1}{\omega_{ci}}\frac{\partial}{\partial t}\left(\rho_s^2\nabla^2\frac{e\phi}{T_e}-\frac{e\phi}{T_e}\right)-\left[\left(\rho_s\nabla \frac{e\phi}{T_e}\times \mathbf{\hat z}\right)\cdot\rho_s\nabla\right]\left[\rho_s^2\nabla^2\frac{e\phi}{T_e}-ln\left(\frac{n_0}{\omega_{ci}}\right)\right]=0](images/math/2/b/9/2b989c6b033a68374031e9f0e9084305.png)
![\left[A,B\right] \equiv \frac{\partial A}{\partial x}\frac{\partial B}{\partial y}-\frac{\partial A}{\partial y}\frac{\partial B}{\partial x}](images/math/e/c/a/eca100de9bde18594f10d168d15ac814.png)
![\frac{\partial}{\partial t}\left(\nabla^2\phi-\phi\right)-\left[\phi,\nabla^2\phi\right]-\left[\phi,ln\left(\frac{n_0}{\omega_{ci}}\right)\right]=0](images/math/7/2/a/72a17e1588d29acd7ea5baca14c846ac.png)
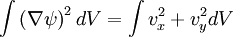
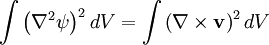
![\int\left[\phi^2+\left(\nabla\phi\right)^2\right]dV](images/math/d/a/e/dae4520437787d7a34d2b22d6e2633a7.png)
![\int\left[\left(\nabla\phi\right)^2+\left(\nabla^2\phi\right)^2\right]dV](images/math/5/1/1/51175d928866734eb26fc33cae75f93f.png)


