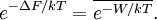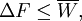To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Jarzynski equalityThe Jarzynski equality (JE) is an equation in statistical mechanics that relates free energy differences between two equilibrium states and non-equilibrium processes. It is named after the physicist Christopher Jarzynski (then at Los Alamos National Laboratory) who discovered it in 1997. Product highlightIn thermodynamics, the free energy difference ΔF = FB − FA between two states A and B is connected to the work W done on the system through the inequality:
the equality happening only in the case of a quasistatic process, i.e. when one takes the system from A to B infinitely slowly. In contrast to the thermodynamic statement above, the JE remains valid no matter how fast the process happens. The equality itself can be straightforwardly derived from the Crooks fluctuation theorem and is presented below, followed by a brief explanation of the terms and notation: Here k is the Boltzmann constant and T is the temperature of the system in the equilibrium state A (or, equivalently, the temperature of the heat reservoir with which the system was thermalized before the process took place). The over-line indicates an average over all possible realizations of a process that takes the system from the equilibrium state A to the equilibrium state B.1 In the case of an infinitely slow process, the work W performed on the system in each realization is numerically the same, so the average becomes irrelevant and the Jarzynski equality reduces to the thermodynamic equality ΔF = W (see above). In general, however, W depends upon the specific initial microstate of the system, though its average can still be related to ΔF through an application of Jensen's inequality in the JE, viz. in accordance with the second law of thermodynamics. Since its original derivation, the Jarzynski equality has been verified in a variety of contexts, ranging from experiments with biomolecules to numerical simulations. Many other theoretical derivations have also appeared, lending further confidence to its universality. An issue of current debate is whether the Jarzynski equality was published already in 1977 by the Russian physicists G.N. Bochkov and Yu. E. Kuzovlev (see Bibliography). These authors proposed a generalized version of the Fluctuation-Dissipation relations which holds even in the presence of arbitrary external time-dependent forces. The generalized Fluctuation-Dissipation relations take on a similar form as the more recently proposed fluctuation theorem. Notes
Bibliography
See also
Categories: Statistical mechanics | Non-equilibrium thermodynamics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Jarzynski_equality". A list of authors is available in Wikipedia. |





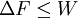 ,
,