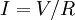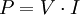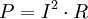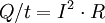To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Joule's lawsJoule's laws are a pair of laws concerning the heat produced by a current and the energy dependence of an ideal gas to that of pressure, volume, and temperature, respectively. Product highlightJoule's first law, also known as the Joule effect, is a physical law expressing the relationship between the heat generated by the current flowing through a conductor. It is named for James Prescott Joule who studied the phenomenon in the 1840s. It is expressed as: Where Q is the heat generated by a constant current I flowing through a conductor of electrical resistance R, for a time t. When current, resistance and time are expressed in amperes, ohms, and seconds respectively, the unit of Q is the joule. Joule's first law is sometimes called the Joule-Lenz law since it was later independently discovered by Heinrich Lenz. The heating effect of conductors carrying currents is known as Joule heating. Joule's first law is closely related to, and thus easily derived from Ohm's Law. Below is a quick synopsis of how these two laws relate, for detailed information see Ohm's Law. Joule's second law states that the internal energy of an ideal gas is independent of its volume and pressure, depending only its temperature. Relation to Ohm's LawJoule's first law is closely related to, and thus easily derived from Ohm's Law. Below is a quick synopsis of how these two laws relate.
Combining the above two equations and putting them in terms of the I and R:
For more information on Power see Power (physics). Finally the amount of power dissipated by a resistor is the amount of work done on the resistor (ie. heat dissipated in the resistor) divided by the length of time: Which therefore gives: Note that Joule's first law could also be written in terms of the voltage across the resistor: See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Joule's_laws". A list of authors is available in Wikipedia. |





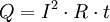
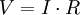 or
or