To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Lattice Boltzmann methodsLattice Boltzmann methods or LBM is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solving the Navier-Stokes equations, the discrete Boltzmann equation is solved to simulate the flow of a Newtonian fluid with collision models such as Bhatnagar-Gross-Krook (BGK). By simulating the interaction of a limited number of particles the viscous flow behavior emerges automatically from the intrinsic particle streaming and collision processes. Product highlight
AlgorithmLBM is a relatively new simulation technique for complex fluid systems and has attracted interest from researchers in computational physics. Unlike the traditional CFD methods, which solve the conservation equations of macroscopic properties (i.e., mass, momentum, and energy) numerically, LBM models the fluid consisting of fictive particles, and such particles perform consecutive propagation and collision processes over a discrete lattice mesh. Due to its particulate nature and local dynamics, LBM has several advantages over other conventional CFD methods, especially in dealing with complex boundaries, incorporating of microscopic interactions, and parallelization of the algorithm. Development from the LGA methodLBM originated from the Lattice Gas Automata (LGA) method, which can be considered as a simplified fictitious molecular dynamics model in which space, time, and particle velocities are all discrete. Each lattice node is connected to its neighbors by 6 lattice velocities, using for example the hexagonal FHP model. There can be either 0 or 1 particles at a lattice node moving in a lattice direction. After a time interval, each particle will move to the neighboring node in its direction, this process is called the propagation or streaming step. When there are more than one particles arriving at the same node from different directions, they collide and change their directions according to a set of collision rules. Suitable collision rules should conserve the particle number (mass), momentum, and energy before and after the collision. However, it was found that LGA suffers from several native defects: lack of Galilean invariance, statistical noise, exponential complexity for three-dimensional lattices, etc. The main motivation for the transition from LGA to LBM was the desire to remove the statistical noise by replacing the Boolean particle number in a lattice direction with its ensemble average, the so-called density distribution function. Accompanying this replacement, the discrete collision rule is also replaced by a continuous function known as the collision operator. In the LBM development, an important simplification is to approximate the collision operator with the Bhatnagar-Gross-Krook (BGK) relaxation term. This lattice BGK (LBGK) model makes simulations more efficient and allows flexibility of the transport coefficients. On the other hand, it has been shown that the LBM scheme can also be considered as a special discretized form of the continuous Boltzmann equation. Through a Chapman-Enskog analysis, one can recover the governing continuity and Navier-Stokes equations from the LBM algorithm. In addition, the pressure field is also directly available from the density distributions and hence there is no extra Poisson equation to be solved as in traditional CFD methods. Lattices and the DnQm classificationLattice Boltzmann models can be operated on a number of different lattices, both cubic and triangular, and with or without rest particles in the discrete distribution function. A popular way of classifying the different methods by lattice is the DnQm scheme. Here "Dn" stands for "n dimensions" while "Qm" stands for "m speeds". For example, D3Q15 is a three-dimensional Lattice Boltzmann model on a cubic grid, with rest particles present. Each node has a crystal shape, and can deliver particles to each of the six neighboring nodes which share a surface, the eight neighboring nodes sharing a corner, and itself.[1] (The D3Q15 model does not contain particles moving to the twelve neighboring nodes which share an edge; adding those would create a "D3Q27" model.) Simulation of mixturesSimulating multiphase/multicomponent flows has always been a challenge to conventional CFD because of the moving and deformable interfaces. More fundamentally, the interfaces between different phases (liquid and vapor) or components (e.g, oil and water) originate from the specific interactions among fluid molecules. Therefore it is difficult to implement such microscopic interactions into the macroscopic Navier-Stokes equation. However, in LBM, the particulate kinetics provides a relatively easy and consistent way to incorporate the underlying microscopic interactions by modifying the collision operator. Several LBM multiphase/multicomponent models have been developed. Here phase separations are generated automatically from the particle dynamics and no special treatment is needed to manipulate the interfaces as in traditional CFD methods. Successful applications of multiphase/multicomponent LBM models can be found in various complex fluid systems, including interface instability, bubble/droplet dynamics, wetting on solid surfaces, interfacial slip, and droplet electrohydrodynamic deformations. LimitationsDespite the increasing popularities of LBM in simulating complex fluid systems, one should also be aware of some limitations of this novel approach. At present, high-Mach number flows in aerodynamics are still difficult for LBM, and a consistent thermo-hydrodynamic scheme is absent. However, as with Navier-Stokes based CFD, LBM methods have been successfully coupled to thermal-specific solutions to enable heat transfer (solids-based conduction, convection and radiation) simulation capability. For multiphase/multicomponent models, the interface thickness is usually large and the density ratio across the interface is small when compared with real fluids. Nevertheless, the wide applications and fast advancements of this method during the past twenty years have proven its potential in computational physics, including microfluidics: LBM demonstrates promising results in the area of high Knudsen number (defined by the ratio of the mean free path between molecules to a geometric length scale) flows.
Mathematical detailsThe Boltzmann equation is an evolution equation for a single particle probability distribution function f(x,v,t): where F is an external force and Ω is a collision integral. The lattice Boltzmann method discretizes this equation by limiting space to a lattice and the velocity space to a discrete set of velocities vi. The discretized Boltmann equation, which is the Lattice Boltzmann equation then reads:
The collision operator is often approximated by a BGK collision operator: where The moments of the fi give the local conserved quantities. The density is given by
and the local momentum is given by
For the popular isothermal lattice Boltmann methods these are the only conserved quantities. Thermal models also conserve energy and therefore have an additional conserved quantity:
The collision operator has to respect the conservation laws. Therefore the equilibirum distribution Software
Further reading
Notes
|
|||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Lattice_Boltzmann_methods". A list of authors is available in Wikipedia. |





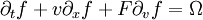
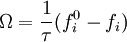
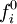 is the local equilibrium distribution.
is the local equilibrium distribution.


