Magneto-optic effect

A magneto-optic effect is any one of a number of phenomena in which an electromagnetic wave propagates through a medium that has been altered by the presence of a quasistatic magnetic field. In such a material, which is also called gyrotropic or gyromagnetic, left- and right-rotating elliptical polarizations can propagate at different speeds, leading to a number of important phenomena. When light is transmitted through a layer of magneto-optic material, the result is called the Faraday effect: the plane of polarization can be rotated, forming a Faraday rotator. The results of reflection from a magneto-optic material are known as the magneto-optic Kerr effect (not to be confused with the nonlinear Kerr effect).

Additional recommended knowledge

How to ensure accurate weighing results every day?

Daily Visual Balance Check

Essential Laboratory Skills Guide

In general, magneto-optic effects break time reversal symmetry locally (i.e. when only the propagation of light, and not the source of the magnetic field, is considered) as well as Lorentz reciprocity, which is a necessary condition to construct devices such as optical isolators (through which light passes in one direction but not the other). (The other, less useful, way to break time reversal symmetry is to rely upon absorption loss.)

Two gyrotropic materials with reversed rotation directions of the two principal polarizations, corresponding to complex-conjugate ε tensors for lossless media, are called optical isomers.

Gyrotropic permittivity

In particular, in a magneto-optic material the presence of a magnetic field (either externally applied or because the material itself is ferromagnetic) can cause a change in the permittivity tensor ε of the material. The ε becomes anisotropic, a 3×3 matrix, with complex off-diagonal components, depending of course on the frequency ω of incident light. If the absorption losses can be neglected, ε is a Hermitian matrix. The resulting principal axes become complex as well, corresponding to elliptically-polarized light where left- and right-rotating polarizations can travel at different speeds (analogous to birefringence).

More specifically, for the case where absorption losses can be neglected, the most general form of Hermitian ε is:

or equivalently the relationship between the displacement field D and the electric field E is:

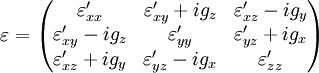
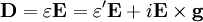
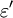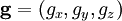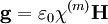
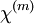where is a real symmetric matrix and is a real pseudovector called the gyration vector, whose magnitude is generally small compared to the eigenvalues of . The direction of g is called the axis of gyration of the material. To first order, g is proportional to the applied magnetic field:

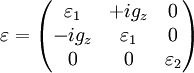
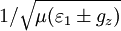where is the magneto-optical susceptibility (a scalar in isotropic media, but more generally a tensor). If this susceptibility itself depends upon the electric field, one can obtain a nonlinear optical effect of magneto-optical parametric generation (somewhat analogous to a Pockels effect whose strength is controlled by the applied magnetic field).

The simplest case to analyze is the one in which g is a principal axis (eigenvector) of , and the other two eigenvalues of are identical. Then, if we let g lie in the z direction for simplicity, the ε tensor simplifies to the form:

Most commonly, one considers light propagating in the z direction (parallel to g). In this case the solutions are elliptically polarized electromagnetic waves with phase velocities (where μ is the magnetic permeability). This difference in phase velocities leads to the Faraday effect.

For light propagating purely perpendicular to the axis of gyration, the properties are known as the Cotton-Mouton effect and used for a Circulator.

See also

• Zeeman effect
• QMR effect
• Magneto-optic Kerr effect
• Voigt Effect

References

• Federal Standard 1037C and from MIL-STD-188
• L. D. Landau and E. M. Lifshitz, Electrodynamics of Continuous Media (Addison-Wesley: Reading, MA, 1960). §82.
• J. D. Jackson, Classical Electrodynamics (3rd. ed) (Wiley: New York, 1998). §6.10.
• F. Jonsson and C. Flytzanis, "Optical parametric generation and phase matching in magneto-optic media," Optics Letters 24 (21), 1514-1516 (1999).