To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Mason-Weaver equationThe Mason-Weaver equation describes the sedimentation and diffusion of solutes under a uniform force, usually a gravitational field.[1] Assuming that the gravitational field is aligned in the z direction (Fig. 1), the Mason-Weaver equation may be written where t is the time, c is the solute concentration (moles per unit length in the z-direction), and the parameters D, s, and g represent the solute diffusion constant, sedimentation coefficient and the (presumed constant) acceleration of gravity, respectively. The Mason-Weaver equation is complemented by the boundary conditions at the top and bottom of the cell, denoted as za and zb, respectively (Fig. 1). These boundary conditions correspond to the physical requirement that no solute pass through the top and bottom of the cell, i.e., that the flux there be zero. The cell is assumed to be rectangular and aligned with the Cartesian axes (Fig. 1), so that the net flux through the side walls is likewise zero. Hence, the total amount of solute in the cell is conserved, i.e., dNtot / dt = 0.
Product highlight
Derivation of the Mason-Weaver equationA typical particle of mass m moving with vertical velocity v is acted upon by three forces (Fig. 1): the
drag force fv, the force of gravity mg and the buoyant force ρVg, where g is the acceleration of gravity, V is the solute particle volume and ρ is the solvent density. At equilibrium (typically reached in roughly 10 ns for molecular solutes), the
particle attains a terminal velocity vterm where the three forces are balanced. Since V equals the particle mass m times its partial specific volume where mb is the buoyant mass. We define the Mason-Weaver sedimentation coefficient
the ratio of s and D equals where kB is the Boltzmann constant and T is the temperature in kelvin. The flux J at any point is given by The first term describes the flux due to diffusion down a concentration gradient, whereas the second term describes the convective flux due to the average velocity vterm of the particles. A positive net flux out of a small volume produces a negative change in the local concentration within that volume Substituting the equation for the flux J produces the Mason-Weaver equation The dimensionless Mason-Weaver equationThe parameters D, s and g determine a length scale z0 and a time scale t0 Defining the dimensionless variables subject to the boundary conditions at the top and bottom of the cell, ζa and ζb, respectively. Solution of the Mason-Weaver equationThis equation may be solved by separation of variables. Defining where acceptable values of β are defined by the boundary conditions at the upper and lower boundaries, ζa and ζb, respectively. Since the T equation has the solution T(τ) = T0e − βτ, where T0 is a constant, the Mason-Weaver equation is reduced to solving for the function P(ζ). The ordinary differential equation for P and its boundary conditions satisfy the criteria for a Sturm-Liouville problem, from which several conclusions follow. First, there is a discrete set of orthonormal eigenfunctions Pk(ζ) that satisfy the ordinary differential equation and boundary conditions. Second, the corresponding eigenvalues βk are real, bounded below by a lowest eigenvalue β0 and grow asymptotically like k2 where the nonnegative integer k is the rank of the eigenvalue. (In our case, the lowest eigenvalue is zero, corresponding to the equilibrium solution.) Third, the eigenfunctions form a complete set; any solution for c(ζ,τ) can be expressed as a weighted sum of the eigenfunctions where ck are constant coefficients determined from the initial distribution c(ζ,τ = 0) At equilibrium, β = 0 (by definition) and the equilibrium concentration distribution is which agrees with the Boltzmann distribution. The P0(ζ) function satisfies the ordinary differential equation and boundary conditions at all values of ζ (as may be verified by substitution), and the constant B may be determined from the total amount of solute To find the non-equilibrium values of the eigenvalues βk, we proceed as follows. The P equation has the form of a simple harmonic oscillator with solutions Depending on the value of βk, ωk is either purely real (
where A and B are constants and ω is real and strictly positive. By introducing the oscillator amplitude ρ and phase φ as new variables, the second-order equation for P is factored into two simple first-order equations Remarkably, the transformed boundary conditions are independent of ρ and the endpoints ζa and ζb Therefore, we obtain an equation giving an exact solution for the frequencies ωk The eigenfrequencies ωk are positive as required, since ζa > ζb, and comprise the set of harmonics of the fundamental frequency Taken together, the non-equilibrium components of the solution correspond to a Fourier series decomposition of the initial concentration distribution c(ζ,τ = 0)
multiplied by the weighting function eζ / 2. Each Fourier component decays independently as See alsoReferences
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Mason-Weaver_equation". A list of authors is available in Wikipedia. |


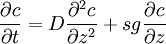
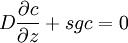
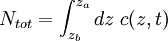



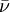 , the equilibrium condition may be written as
, the equilibrium condition may be written as
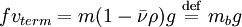
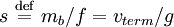 . Since the drag coefficient f is related to the diffusion constant D by the
. Since the drag coefficient f is related to the diffusion constant D by the 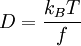 ,
,
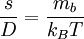

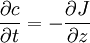
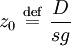
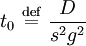
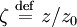 and
and 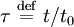 , the Mason-Weaver equation becomes
, the Mason-Weaver equation becomes
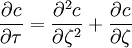
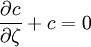
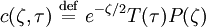 , we obtain the two equations coupled by a constant
, we obtain the two equations coupled by a constant 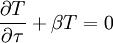
![\frac{\partial^{2} P}{\partial \zeta^{2}} + \left[ \beta - \frac{1}{4} \right] P = 0](images/math/7/3/6/7362c04dd9333370d3b69af7b4106b8c.png)
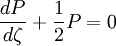
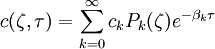
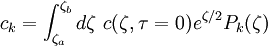
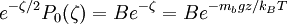
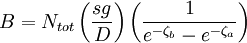
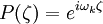 where
where
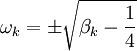
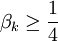 ) or purely imaginary (
) or purely imaginary (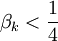 ). Only one purely imaginary solution can satisfy the boundary conditions, namely, the equilibrium solution. Hence, the non-equilibrium eigenfunctions can be written as
). Only one purely imaginary solution can satisfy the boundary conditions, namely, the equilibrium solution. Hence, the non-equilibrium eigenfunctions can be written as
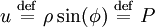
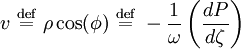
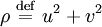
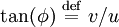
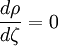
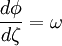
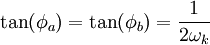
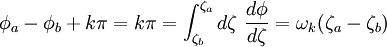
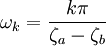
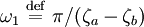 . Finally, the eigenvalues
. Finally, the eigenvalues 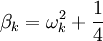
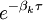 , where
, where 

